20、数据结构和算法 - 实战：多路查找树

定义

多路查找树的特点是其每一个结点的孩子数可以多于两个，且每个结点处可以存储多个元素。所有元素之间存在某种特定的关系。

2-3树

多路查找树中每一个结点都具有两个孩子或者三个孩子称为2-3树。

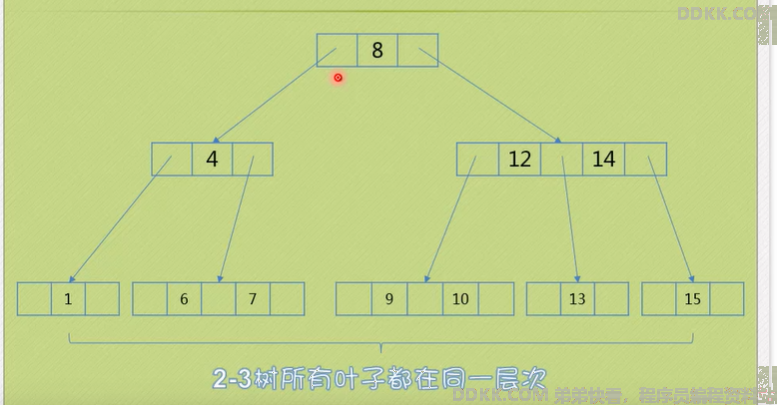
2-3树的插入原理

插入1，正常。
插入5，需要拆分6.7
插入11，需要拆分9.10
… 如果所有的树都是三个节点，那么就需要再深一层

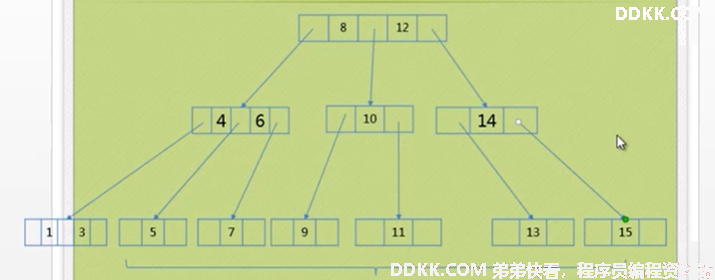
现在插入2，需要增加深度

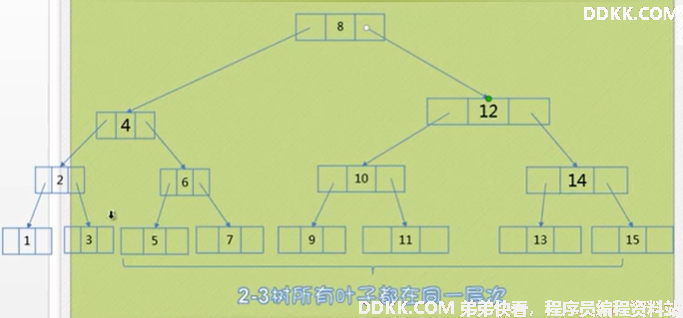
2-3树的删除原理

情况1：如果删除一个双亲是二节点的但是孩子是三个，比如删除1，调整4，6，7的位置。

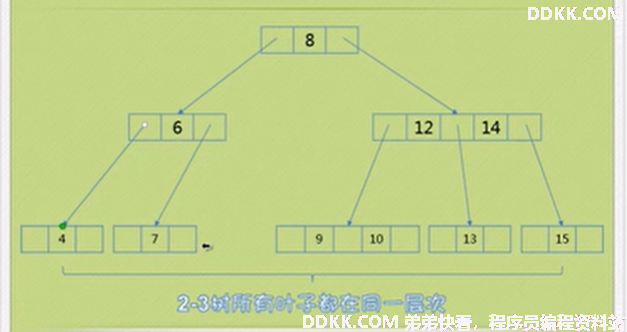
情况2：删除一个双亲是二节点但是孩子是两个，比如删除4，（这里引用一个知识点：根结点的左孩子的最右一个孩子是根结点的直接前驱，同理，直接后继是右孩子的最左孩子。）所以把根结点，直接前驱和后继调整位置。

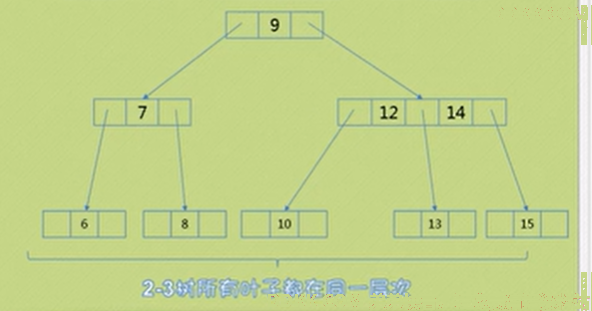
情况3：叶子结点是二节点，双亲是三节点的情况，例如删除10。把双亲变成二节点，调整11，13

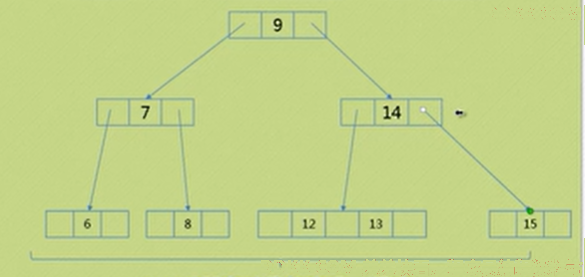
情况4：删除一棵满二叉树的情况，例如下面这种情况：

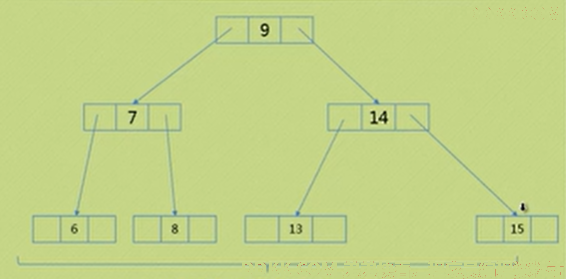
此时如果删除8，所有的二节点不能拆分的情况下，缩小一层深度。

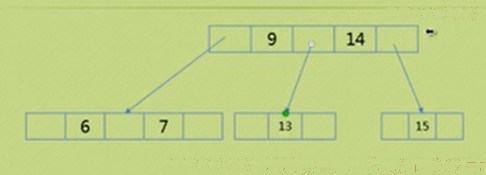
情况5：删除双亲的情况，例如删除4和12。调整6.7和9.10

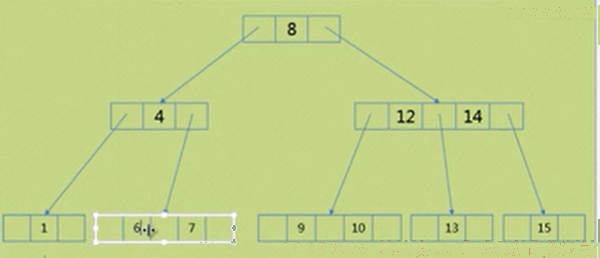
删除后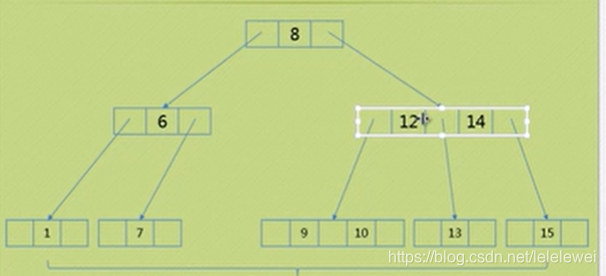 

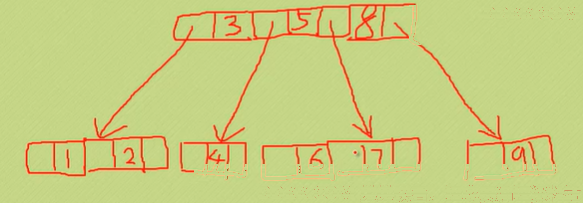
2-3-4树

要求，构建数组{7，1，2，5，6，9，8，4，3}

B树

B树，一种平衡的多路查找树，2-3树和2-3-4树都是B树的特例。

结点最大的孩子树数目称为B树的阶，因此，2-3树是3阶B树，2-3-4树是4阶B树。

一个m阶的B树具有如下属性

• 如果根结点不是叶结点，则其至少有两棵子树。
• 每一个非根的分支都有k-1个元素（关键字）和k个孩子，其中k满足m/2（向上取整）<= k <= m
• 所有叶子节点处于同一个层次
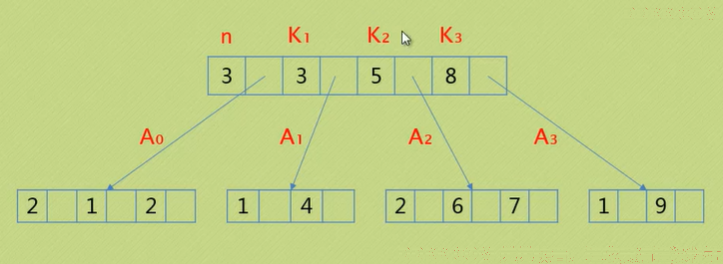
• 每一个分支结点包含下列信息数据
  n，A0,K1,A1,K2,A2,K3…
  (K是关键字，Ki<Ki+1,Ai指向子树根结点的指针）