09、数据结构和算法 - 实战:递归和分治
递归
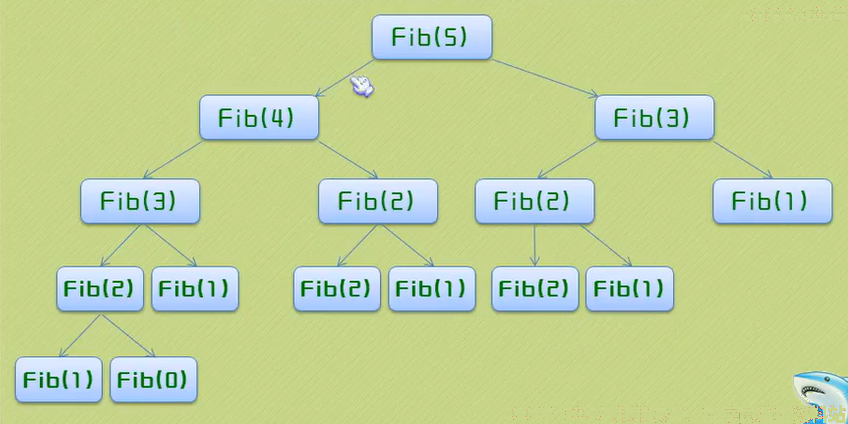
斐波那契数列的递归实现
斐波那契数列为:1,1,2,3,5,8,13,21,34,55,89,144…
用迭代的思想编写打印前40位的数列的代码。
#include <stdio.h>
#include <math.h>
int main()
{
int i;
int a[40];
a[0] = 1;
a[1] = 1;
printf("%d %d",a[0],a[1]);
for(i = 2;i < 40; i++)
{
a[i] = a[i-1] + a[i-2];
printf("%d ",a[i]);
}
return 0;
}
用递归的思想编写代码(函数自己调用自己)
int Fib(int i)
{
if(i < 2 )
return i == 0 ? 0:1;
return Fib(i - 1) + Fib(i - 2);
}
定义
把一个直接调用自己或者通过一系列调用语句间接地调用自己的函数,称为递归函数。
注意:不能陷入永不结束的循环中,所以必须至少有一个条件,当满足这个条件时递归不再进行。
对比刚才的斐波那契数列。迭代使用循环结构,递归使用选择结构。使用递归能使程序的结构更清晰简洁,减少读懂代码的时间。
缺点:大量的递归会建立函数的副本,消耗大量的内存和时间。
代码:计算n的阶乘。
int factorial(n)
{
if( 0 == n)
return 1;
else
return n*factorial(n - 1)
}
例子
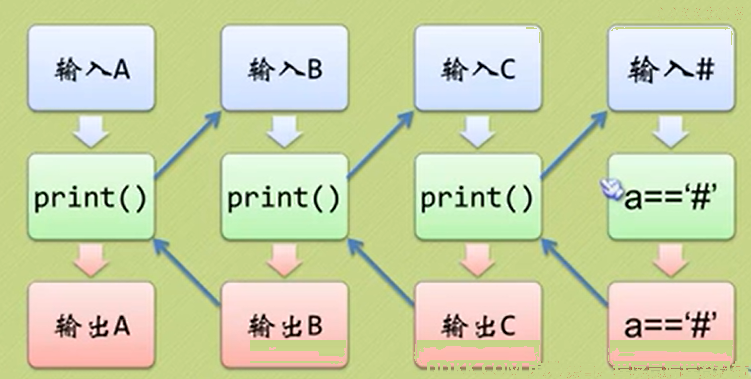
编写一个递归函数,将输入的任意长度的字符串反向输出。结束条件为#
void print()
{
char a;
scanf("%c", &a);
if(a != '#')
print();
if(a != '#')
printf("%c",a );
}
分治
当一个问题规模较大并且不易求解的时候,就可以考虑将问题分为几个小的模块,逐一解决。
折半查找算法
一种常用的查找方法,该方法通过不断缩小一半的查找范围,直到达到目的,效率较高。实际上也是一个递归的过程,每次都将问题的规模减少为原来的一半,缩小后的子问题和原问题类型保持一致。
汉诺塔
在世界中心贝拿勒斯的圣庙里,一块黄铜板上插着三根宝石针。印度教的主神梵天在创造世界的时候,在其中一根针上从下到上地穿好了由大到小的64片金片,这就是所谓的汉诺塔。不论白天黑夜,总有一个僧侣在按照下面的法则移动这些金片,一次只移动一片,不管在哪根针上,小片必须在大片上面。

思路:
1、 先将63个盘子移动到Y上,确保大盘在小盘下面,;
2、 再将最底下的64个移动到Z上,;
3、 最后将Y上的63个移动到Z上;
总结有两个问题需要解决
问题一,将X上的63个盘子借助Z移动到Y上。
问题二:将Y上的63个盘子借助X移动到Z上。
#include <stdio.h>
//将n个盘子从x借助y移动到z
void move(int n,char x, char y, char z)
{
if(1 == a )
{
printf("%c-->%c\n",x,z);
}
else
{
move(n-1,x,z,y); //将n-1个盘子从x借助z移动到y上
printf("%c-->%c\n",x,z);//将第n个盘子从x移动到z上
move(n-1,y,x,z);//将n-1个盘子从y借助x移动到z上
}
}
int main()
{
int n;
printf("请输入汉诺塔的层数:\n");
scanf("%d",&n);
printf("移动的步骤如下\n");
move(a, 'X', 'Y', 'Z');
return 0;
}
八皇后问题
回溯算法的典型例题(在这里用递归算法求解)
在8*8的国际象棋上摆放八个皇后,使其不能相互攻击,任意皇后不能处于同一行,同一列或者同一斜线上,请问有多少种摆法。(92种)

#include <stdio.h>
int count = 0;
int notDanger(int row , int j, int (*chess)[8])
{
int i , k , flag1 = 0,flag2 = 0,flag3 = 0,flag4 = 0,flag5 = 0;
//判断列方向
for(i = 0; i < 8; i ++)
{
if( *(*(chess + i) + j) != 0)
{
flag1 = 1;
break;
}
}
//判断左上方
for(i = row, k = j;i>=0&& k>=0; i--,k--)
{
if( *(*(chess + i) + k) != 0)
{
flag2 = 1;
break;
}
}
//判断右下方
for(i = row, k = j;i < 8 && k < 8; i++,k++)
{
if( *(*(chess + i) + k) != 0)
{
flag3 = 1;
break;
}
}
//判断右上方
for(i = row, k = j;i>=0&& k< 0; i--,k++)
{
if( *(*(chess + i) + k) != 0)
{
flag4 = 1;
break;
}
}
//判断左下方
for(i = row, k = j;i < 8 && k >= 0; i++,k++)
{
if( *(*(chess + i) + k) != 0)
{
flag5 = 1;
break;
}
}
if(flag1 ||flag2 ||flag3 ||flag4 ||flag5 )
{
return 0;
}
else
return 1;
}
//参数row表示起始行,n表示列数,*chess[8]表示指向棋盘每一行的指针
void EightQueen(int row,int n,int (*chess)[8])
{
int chess2[8][8];
int i ,j;
for(i = 0; i < 8; i ++)
{
for(j = 0; j < 8; j++)
{
chess2[i][j] = chess[i][j];
}
}
if(8 == row)
{
printf("第%d种方案:",count + 1);
for(i = 0; i < 8; i ++)
{
for(j = 0; j < 8; j++)
{
printf("%d\t",*(*(chess2+i)+j));
}
printf("\n");
}
printf("\n");
}
else
{
//判断这个位置是否有危险
//如果没有危险,继续。
for(j = 0; j < n; j++)
{
if(notDanger(row , j, chess))
{
for(i = 0; i <8; i++)
{
*(*(chess2 + row)+i) = 0;
}
*(*(chess2 + row)+j) = 1;
EightQueen(row + 1 ,n ,chess2);
}
}
}
}
int main()
{
int chess[8][8];
int i,j;
for(i = 0; i < 8; i ++)
{
for(j = 0; j < 8; j++)
{
chess[i][j]=0;
}
}
EightQueen( 0, 8 , chess );
printf("总共有%d种解决方法\n",count);
return 0;
}