14、数据结构和算法 - 实战:图
图
定义
图(Graph)是由顶点的有穷非空集合和顶点之间边的集合组成,通常表示为G(V,E),其中G表示一个图,V是图G中顶点的集合,E是图G中边的集合。
注意:
1、 图中数据元素称为顶点(Vertex);
2、 强调图的顶点集合V要有穷非空;
3、 图中,任意两个顶点都可能有关系,逻辑关系用边来表示,边集可以是空的;
无向边:顶点Vi和Vj之间的边没有方向,用无序偶(Vi,Vj)表示;
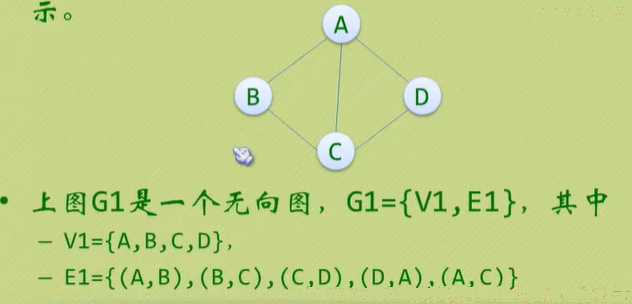
无向边:顶点Vi和Vj之间的边有方向,也称为弧(Arc),用有序偶<Vi,Vj>表示;Vi称为弧尾,Vj称为弧头。
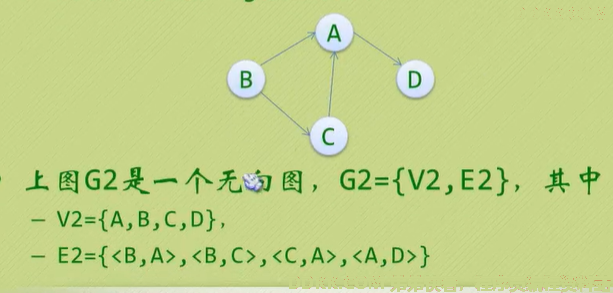
简单图:在图结构中,不存在顶点到其自身的边,且同一条边不重复出现,则称这样的图为简单图。
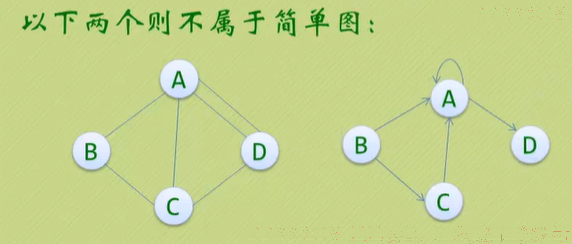
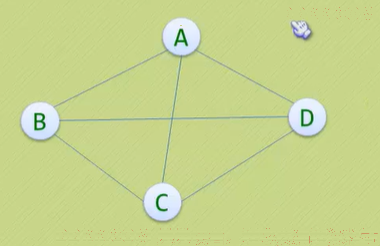
无向完全图:无向图中,如果任意两个顶点之间都存在边,则称该图为无向完全图。含有n个顶点的无向完全图有n*(n-1)/2;
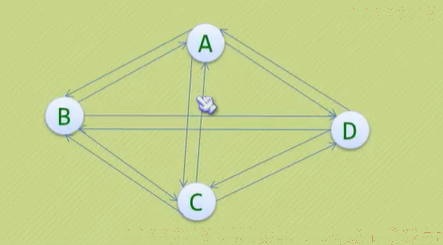
有向完全图:在有向图中,如果任意两个顶点之间都存在方向互为相反的两条弧,则称该图为有向完全图。含有n个顶点的有向完全图有n*(n-1)条边
稀疏图和稠密图:这里的稀疏和稠密是模糊的概念,都是相对而言的,通常认为边或弧数小于n*logn的是稀疏图。
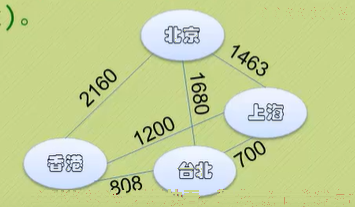
权:有些图的边或弧带有与他相关的数字,带权的图称为网
子图:顶点包含,并且边也包含的,就称为子图。
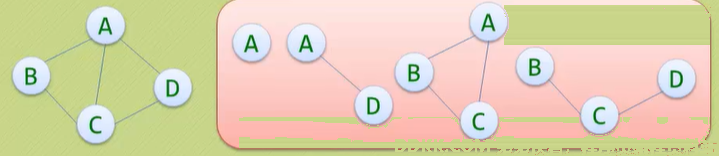
其他的相关概念
1、 对于无向图G=(V,E),如果边(V1,V2)∈E,则称顶点V1和V2互为邻接点,即V1和V2相邻接边(V1,V2)依附于顶点V1和V2,或者说边(V1,V2)与顶点V1和V2相关联;
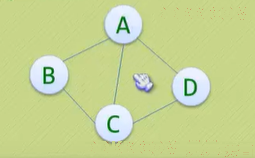
2、 度:顶点V的度是和V相关联的边的数目,记作TD(V);
 3、 对于有向图G=(V,E),如果弧<V1,V2>∈E,则称顶点V1邻接点到顶点V2顶点V2邻接自顶点V1;
3、 对于有向图G=(V,E),如果弧<V1,V2>∈E,则称顶点V1邻接点到顶点V2顶点V2邻接自顶点V1;
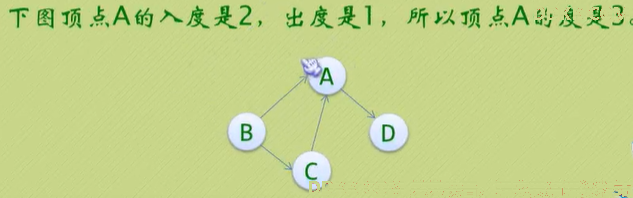
4、 入度:以顶点V为头的弧的数目,记为ID(V);
入度:以顶点V为尾的弧的数目,记为OD(V)
度:TD(V) = ID(V) + OD(V)
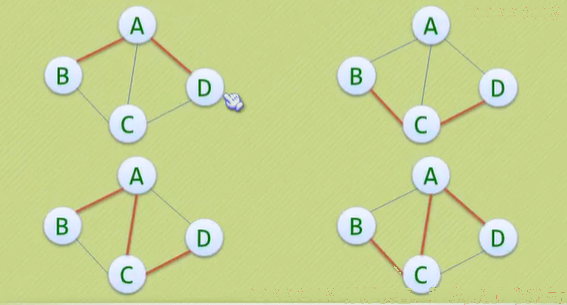
 5、 路径:无向图G=(V,E)中从顶点V1到顶点V2的路径;
5、 路径:无向图G=(V,E)中从顶点V1到顶点V2的路径;
 6、 如果G是有向图,则路径也是有向的;
6、 如果G是有向图,则路径也是有向的;
7、 回路或环:第一个和最后一个顶点相同;
8、 简单环:序列中顶点不重复出现的路径称为简单路径;
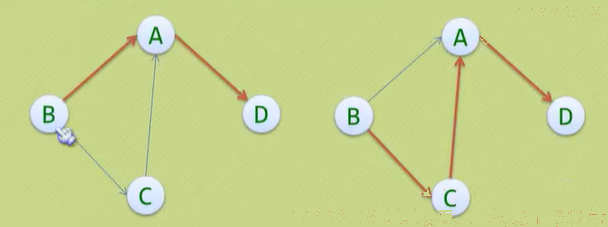

1、 连通图:在无向图G中,如果顶点V1,和V2有路径,则称V1,V2是连通的,如果图中任意两个顶点都是连通的,则称G是连通图;
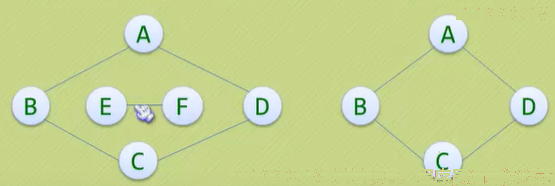 2、 连通分量:无向图中的极大连通子图称为连通分量(注意:子图并且要连通);
2、 连通分量:无向图中的极大连通子图称为连通分量(注意:子图并且要连通);
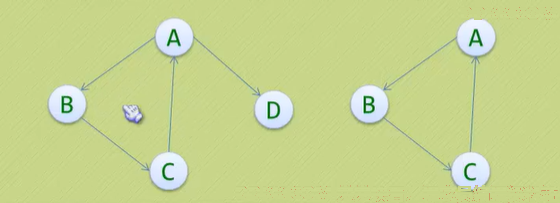
3、 强连通图:有向图G,每一对顶点都存在路径;
4、 强连通分量:有向图中的极大连通子图称为连通分量(注意:子图并且要连通);
 5、 连通图的生成树:是一个极小的连通子图,包含图中全部的n的顶点,但只有足以构成一棵树的n-1条边;
5、 连通图的生成树:是一个极小的连通子图,包含图中全部的n的顶点,但只有足以构成一棵树的n-1条边;
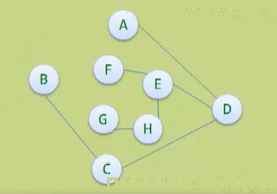 6、 有向树:有向图恰有一个顶点入度为0,其余顶点的入度均为1,则是一棵有向树;
6、 有向树:有向图恰有一个顶点入度为0,其余顶点的入度均为1,则是一棵有向树;
图的存储结构
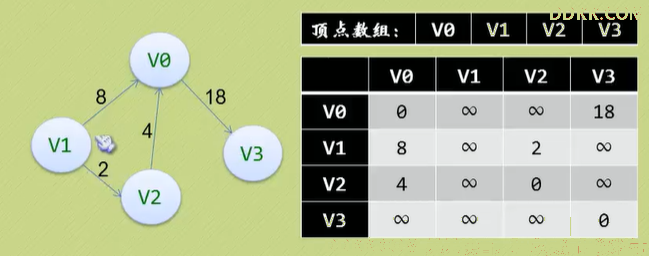
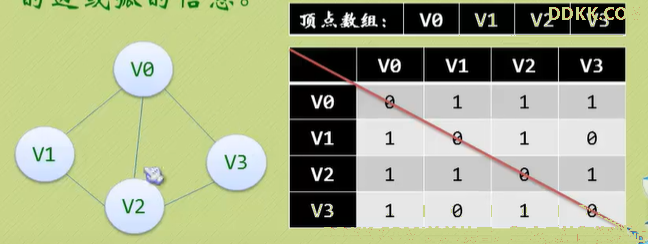
邻接矩阵(无向图)
用两个数组来表示,一个一维数组存储图中顶点信息,一个二维数组(称为邻接矩阵,也是对称矩阵)存储图中的边或弧的信息。
邻接矩阵(有向图)
与无向图不同,有向图的邻接矩阵不对称。入度是列的和,出度为行的和
邻接矩阵(网)