12、数据结构和算法 - 实战:线索二叉树
线索二叉树
普通二叉树的缺点:浪费空间,浪费运行时间
改进:每个结点定义前驱和后继结点。
将学习笔记(十一)中的结构体扩充为以下结构:

ltag为0时指向该结点的左孩子,为1表示指向该结点的前驱
rtag为0时指向该结点的右孩子,为1表示指向该结点的后继
代码如下
#include <stdio.h>
#include <stdlib.h>
typedef char Elemtype;
//线索存储标志位,link表示指向指针,Thread表示指向前驱或者后继的线索
typedef enum{
Link, Thread} PointerTag;
typedef struct BiThreadNode
{
char data;
struct BiThreadNode *lchild, *rchild;
PointerTag ltag;
PointerTag rtag;
}BitThrNode,*BiThrTree;
//全局变量,始终指向刚刚访问过的结点
BiThrTree pre;
//创建一个二叉树,约定用户遵照前序遍历的方式输入
CreateBiTree(BiTree *T)
{
char c;
scanf("%c",c);
if(' ' == c)
{
*T = NULL;
}
else
{
*T = (BiTNode *)malloc(sizeof(BiTNode));
(*T)->data = c;
(*T)->ltag = Link;
(*T)->ltag = Link;
CreateBiTree(& (*T)->lchild);
CreateBiTree(&(*T)->rchild);
}
}
//中序遍历
InThreading(BiThrTree T)
{
if(T)
{
InThreading(T->lchild); //递归左孩子线索化
if(!T->lchild) //该结点没有左孩子,设置ltag为thread,并把lchild指向前驱
{
T->ltag = Thread;
T->lchild = pre;
}
//结点处理
if(!pre->lchild) //该结点没有左孩子,设置ltag为thread,并把lchild指向前驱
{
pre->rtag = Thread;
pre->rchild = T;
}
pre = T;
InThreading(T->rchild); //递归右孩子线索化
}
}
InOrderThreading(BitThrTree *p, BitThrTree T)
{
*p = (BitThrTree)malloc(sizeof(BitThrNode));
(*p)->ltag = Link;
(*p)->rtag = Thread;
(*p)->rchild = *p;
if(!T)
{
(*p)->lchild = *p;
}
else
{
(*p)->lchild = T;
pre = *p;
InThreading(T);
}
}
void visit(char c)
{
printf("%c",c);
}
//中序遍历,非递归
void InOrderTravel(BiThrTree T)
{
BiThrTree p;
p = T->lchild;
while(p != T)
{
while(p->ltag == Link)
{
p = p->lchild;
}
visit(p->data);
while(p->rtag == Thread && p->rchild != T)
{
p = p->rchild;
visit(p->data);
}
p = p->rchild;
}
}
int main()
{
BiThrTree T =NULL;
CreateBiTree(& T );
InOrderThreading(&P,T);
printf("中序遍历输出结果为:");
InOrderTravel(P);
return 0;
}
树,森林以及二叉树的相互转换
普通树转换为二叉树
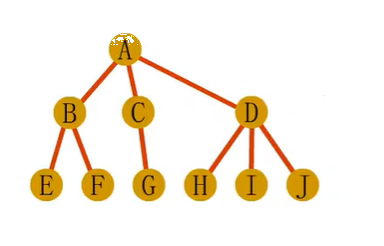
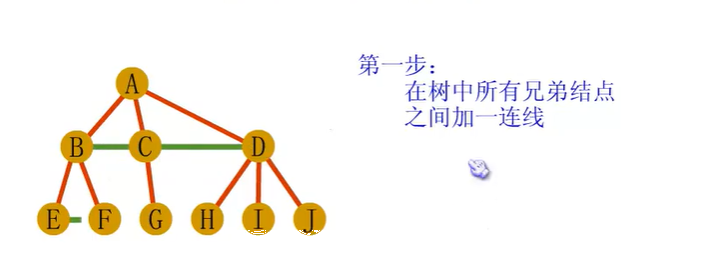
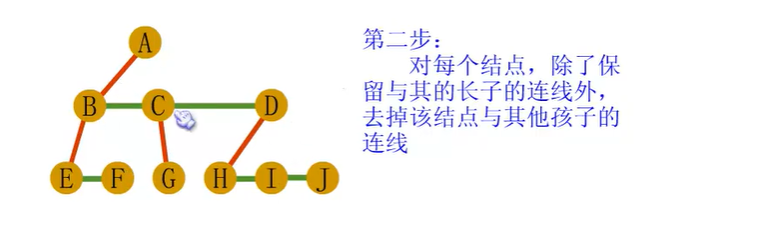
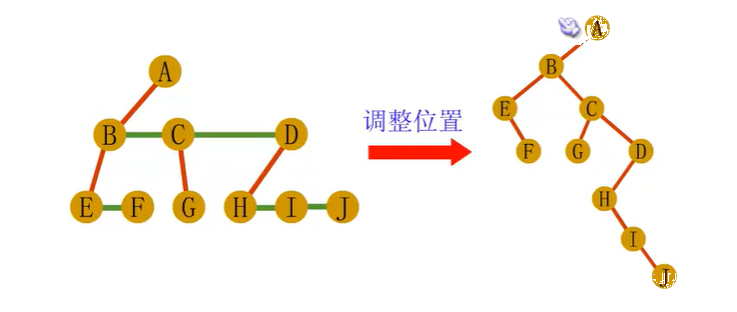
森林到二叉树的转化
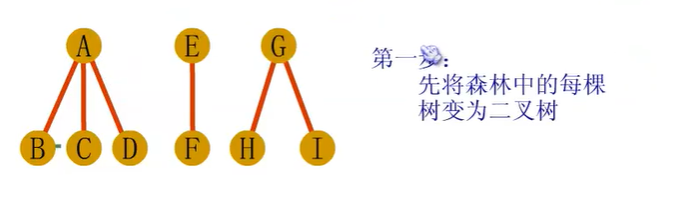
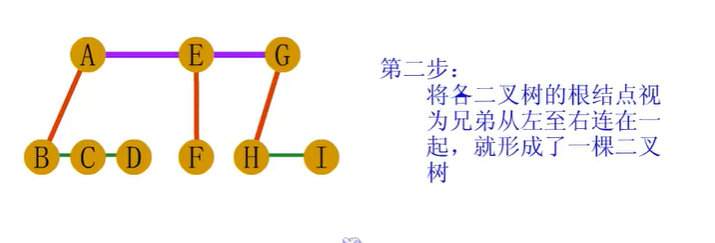
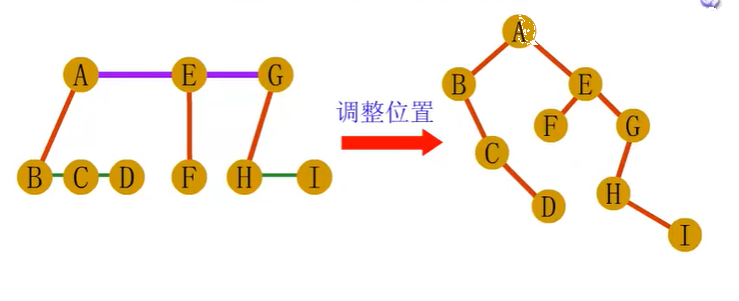
二叉树到树、森林的转换
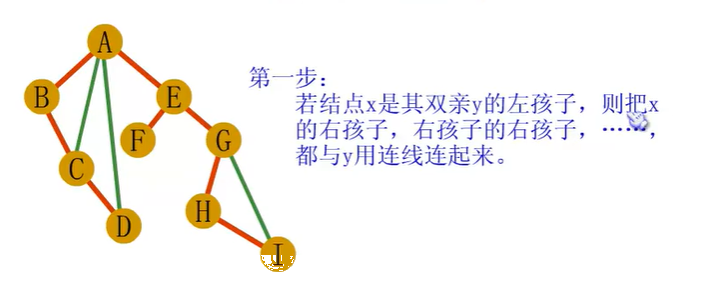
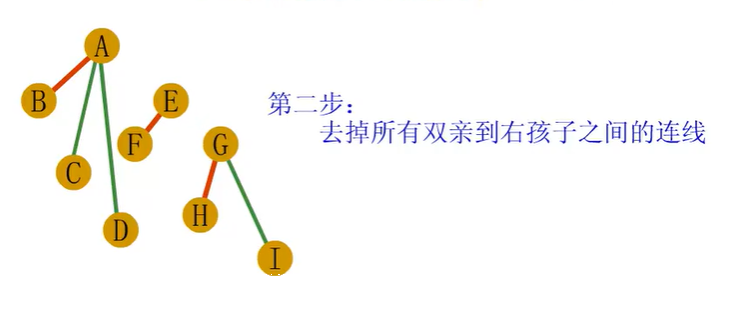
树和森林的遍历
树的遍历
两种,一种是先根遍历,另一种是后根遍历
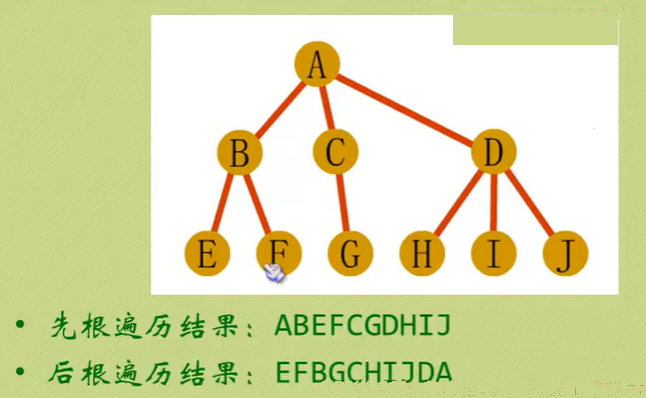
森林的遍历
分为前序遍历和后序遍历
注意:树、森林的前序(根)遍历和二叉树的前序遍历结果相同,后根(序)遍历和二叉树中的中序遍历结果相同。