19、数据结构和算法 - 实战：平衡二叉排序树

定义

要么是一棵空树，要么就左子树和右子树都是平衡二叉树，且左子树和右子树的深度之差的绝对值不超过1。
举几个例子

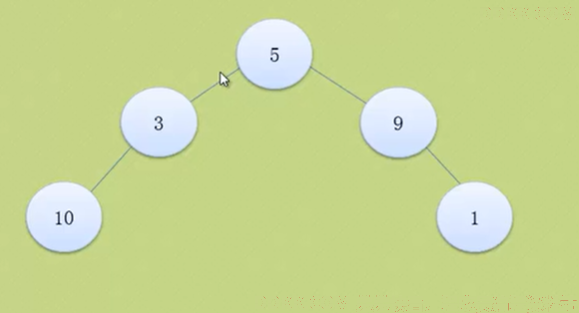
这个不是，因为他不是一棵树。

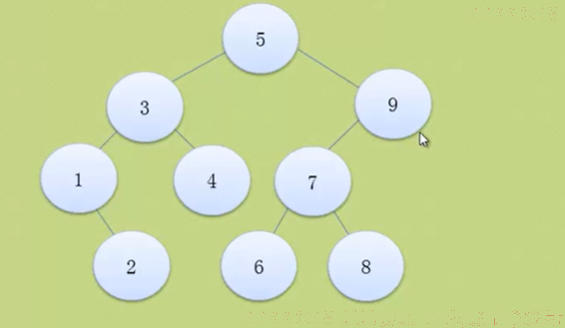
这个也不是，左子树和右子树的差为2.

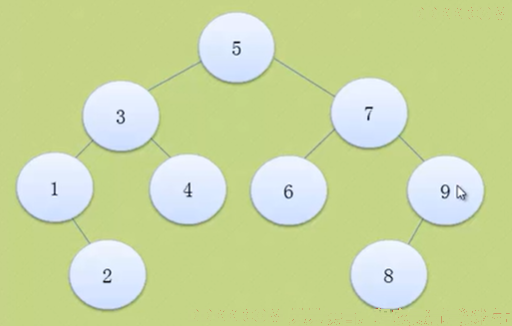
这个就是平衡二叉树

实现

typedef struct BiTNode
{
   
     
	int data;
	int bf;
	struct BiTNode *lchild,*rchild;
}BiTNode, *BiTree;
int InsertAVL(BiTree *T, int e, int *taller)
{
   
     
	if( !*T)
	{
   
     
		*T = (BiTree)malloc(sizeof(BiTNode));
		(*T)->data = e;
		(*T)->lchild = (*T)->rchild = NULL;
		(*T)->bf = EH;
		*taller = TRUE;
	}
	else
	{
   
     
		if( e == (*T)->data)
		{
   
     
			*taller = FALSE;
			return FALSE;
		}
		if( e < (*T)->data)
		{
   
     
			if( !InsertAVL(&(*T->lchild,e , taller))
			{
   
     
				return FALSE;
			}
			if(*taller)
			{
   
     
				switch((*T)->bf)
				{
   
     
					case LH://左边的高
						LeftBalance(T);
						*taller = FALSE;
						break;
					case EH:
						(*T)->bf = LH;
						*taller = TRUE;
						break;
					case RH:
						(*T)->bf = EH;
						*taller = FALSE;
						break;
				}
			}
		}
		else
		{
   
     
			if( !InsertAVL(&(*T->rchild,e , taller))
			{
   
     
				return FALSE;
			}
			if(*taller)
			{
   
     
				switch((*T)->bf)
				{
   
     
					case LH://左边的高
						(*T)->bf = EH;
						*taller = FALSE;
						break;
					case EH:
						(*T)->bf = RH;
						*taller = TRUE;
						break;
					case RH:
						RightBalance(T);
						*taller = FALSE;
						break;
				}
			}
		}
	}
}
void R_Rotate(BiTree *p)
{
   
     
	BiTree L;
	L = (*p)->lchild;
	(*p)->lchild = L->rchild;
	L->rchild = (*p);
	*p=L;
}
void L_Rotate(BiTree *p)
{
   
     
	BiTree L;
	L = (*p)->rchild;
	(*p)->rchild = L->lchild;
	L->lchild = (*p);
	*p=L;
}
void LeftBalance(BiTree *T)
{
   
     
	BiTree L, Lr;
	L= (*T)->lchild;
	
	switch(L->bf)
	{
   
     
		case LH:
			(*T)->bf = L->bf = EH;
			R_Rotate(T);
			break;
		case RH:
			Lr = L->rchild;
			switch(L->bf)
			{
   
     
				case LH:
					(*T)->bf = RH;
					L->bf = EH;
					break;
				case EH:
					(*T)->bf = L->bf = EH;
					break;
				case RH:
					(*T)->bf = EH;
					L->bf = 
					break;
			}
			Lr->bf = EH;
			L_Rotate(&(*T)->lchild); //左旋转
			R_Rotate(T);// 右旋转
	}
}