16、数据结构和算法 - 实战:拓扑排序和关键路径
拓扑排序
无环图:一个无环的有向图,简称DAG图。
AOV网:在一个表示工程的有向图中,用顶点表示活动,弧表示活动之间的优先关系,这样的有向图为顶点表示活动的网,称之为AOV网。
拓扑序列:设G(V, E)是一个具有n个顶点的有向图,V中的顶点序列V1,V2…Vn满足若从顶点Vi到Vj有一条路径,则在顶点序列中顶点Vi必在顶点Vj之前,则我们称这样的顶点序列为一个拓扑序列。
拓扑排序:对一个有向图构造拓扑序列的过程。
拓扑排序算法
方法和步骤如下:
1、 从AOV网中选择一个没有前驱的顶点(该顶点的入度为0),并且输出;
2、 从网中删去该顶点,并且删除从该顶点发出的全部有向边;
3、 重复上述两步,直到剩余网中不再存在没有前驱顶点为止;
可以用邻接表的数据结构表示
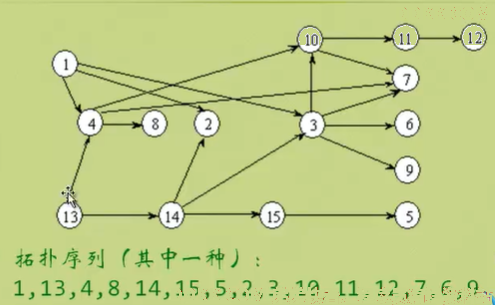
表示为邻接表
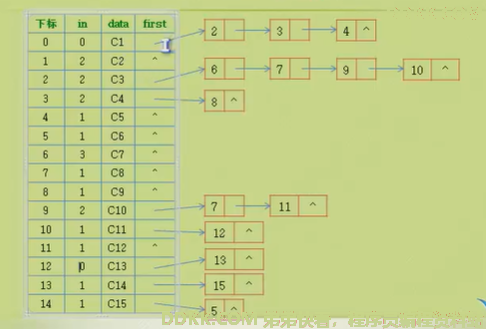
部分代码实现:
//边表结点声明
typedef struct EdgeNode
{
int adjvex;
struct EdgeNode *next;
}EdgeNode;
//顶点表结点声明
typedef struct VertexNode
{
int in;
int data;
EdgeNode *firstedge;
}VertexNode, AdjList[MAXVEX];
typedef struct
{
AdjList adjList;
int numVertexes,numEdges;
}graphAdjList,*GraphAdjList;
//拓扑排序算法
//若GL无回路,则输出拓扑排序序列并返回OK,否则返回ERROR
Status TopologicalSort(GraphAdjList GL)
{
EdgeNode *e;
int i ,k, gettop;
int top = 0; //栈指针下标索引
int count = 0; //用于统计输出顶点的个数
int *stack; //存储入度为0的顶点
stack = (int *)malloc(GL->numVertexes *sizeof(int));\
for( i =0; i< GL->numVertexes ;i ++)
{
if( 0 == GL->adjList[i].in)
{
stack[++top] = i; //将度为0的顶点下标入栈
}
}
while( 0 != top )
{
gettop = stack[top--];
printf("%d -> ",GL->adjList[gettop].data);
count ++;
for( e = GL->adjList[gettop].firstedge; e; e= e->next)
{
k = e->adjvex;
//下面的if条件是要点
//将k号顶点邻接点的入度-,因为前驱已经消除
if(!( -- GL->adjList[k].in))
{
stack[++top] = k;
}
}
}
if(count <GL->numVertexes) // 存在环
{
return ERROR;
}
else
{
return OK;
}
}
关键路径
AOE网:在一个表示工程的带权有向图中,用顶点表示事件,用有向边表示活动,用边上的权值表示活动的持续时间,这种有向图的边表示活动的网,我们称为AOE网(Activity On Edge Network).
始点或源点:没有入边的顶点。
终点或汇点:没有出边的顶点。
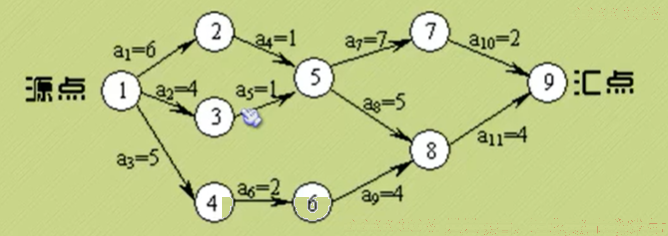
二者的比较(AOE和AOV)

表示完成的流程,全部流程
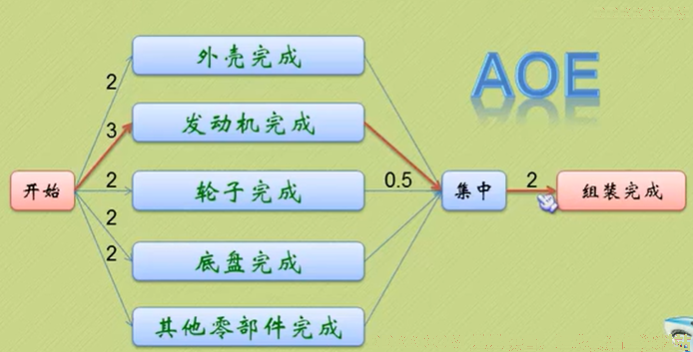
(红色部分是一个关键路径),有一些关键活动。
关键路径算法
一些关键词:
- etv(Earliest Time Of Vertex):时间最早发生时间,就是顶点的最早发生时间
- ltv(Latest Time of Vertex):时间最晚发生时间,就是每个顶点对应的事件最晚需要开始的时间,如果超出此时间将会延误整个工期。
- ete(Earliest Time of Edge):活动的最早开工时间,就是弧的最早发生时间
- lte(Latest Time of Edge):活动的最晚发生时间,就是不推迟工期的最晚开工时间
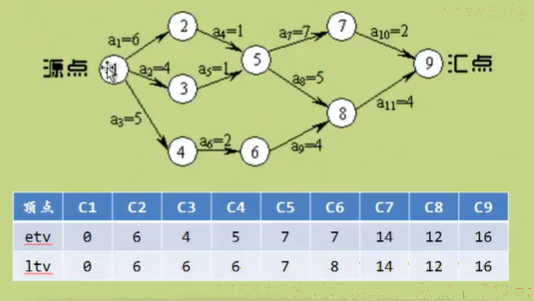
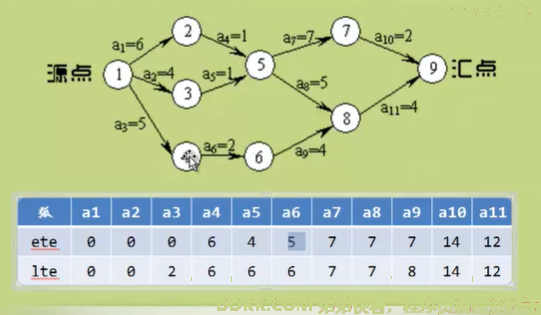
当etv = ltv时,事件的连接就是关键路径。
实现代码如下:
//边表结点声明
typedef struct EdgeNode
{
int adjvex;
struct EdgeNode *next;
}EdgeNode;
//顶点表结点声明
typedef struct VertexNode
{
int in;
int data;
EdgeNode *firstedge;
}VertexNode, AdjList[MAXVEX];
typedef struct
{
AdjList adjList;
int numVertexes,numEdges;
}graphAdjList,*GraphAdjList;
int *etv,*ltv;
int *stack2;
int top2;
//拓扑排序算法
//若GL无回路,则输出拓扑排序序列并返回OK,否则返回ERROR
Status TopologicalSort(GraphAdjList GL)
{
EdgeNode *e;
int i ,k, gettop;
int top = 0; //栈指针下标索引
int count = 0; //用于统计输出顶点的个数
int *stack; //存储入度为0的顶点
stack = (int *)malloc(GL->numVertexes *sizeof(int));
for( i =0; i< GL->numVertexes ;i ++)
{
if( 0 == GL->adjList[i].in)
{
stack[++top] = i; //将度为0的顶点下标入栈
}
}
//初始化etv为0
top2 = 0;
etv = (int * )malloc(GL->numVertexes *sizeof(int));
for( i =0; i< GL->numVertexes ;i ++)
{
etv[i] = 0;
}
stack2 = (int * )malloc(GL->numVertexes *sizeof(int));
while( 0 != top )
{
gettop = stack[top--]; //出栈
//printf("%d -> ",GL->adjList[gettop].data);
count ++;
stack2[top++] = gettop; //保存拓扑序列顺序
for( e = GL->adjList[gettop].firstedge; e; e= e->next)
{
k = e->adjvex;
//下面的if条件是要点
//将k号顶点邻接点的入度-,因为前驱已经消除
if(!( -- GL->adjList[k].in))
{
stack[++top] = k;
}
if(( etv[gettop] +e->weight) > etv[k])
{
etv[k] = etv[gettop] + e->weight;
}
}
}
if(count <GL->numVertexes) // 存在环
{
return ERROR;
}
else
{
return OK;
}
}
//求关键路径,GL为有向图,输出GL的各项关键活动
void CriticalPath(GraphAdiList GL)
{
EdgeNode *e;
int i,gettop, k ,j;
int ete,lte;
TopologicalSort(GL);
//初始化ltv为汇点的时间
ltv = (int * )malloc(GL->numVertexes *sizeof(int));
for( i =0; i< GL->numVertexes ;i ++)
{
ltv[i] = etv[GL->numVertexes - 1];
}
//从汇点倒过来逐个计算
while( 0!= top2)
{
gettop = stack2[top2--];
for( e = GL->adjList[gettop].firstedge; e; e= e->next)
{
k = e->adjvex;
if(ltv[k] - e->weight < ltv[gettop])
{
ltv[gettop] = ltv[k] - e->weight;
}
}
}
//通过etv和ltv求ete和lte
for(j = 0; j < GL->numVertexes ;j ++)
{
for( e = GL->adjList[gettop].firstedge; e; e= e->next)
{
k = e->adjvex;
ete = etv[j];
lte = ltv[k] - e->weight;
if(ete==lte)
printf("<v%d, v%d> length: %d, ",GL->adjList[j].data, GL->adhList[k].data, e->weight);
}
}
}