19、Java JUC源码分析 - 队列-PriorityBlockingQueue
PriorityBlockingQueue是一个基于数组实现的线程安全的无界队列,原理和内部结构跟PriorityQueue基本一样,只是多了个线程安全。javadoc里面提到一句,1:理论上是无界的,所以添加元素可能导致outofmemoryerror;2.不容许添加null;3.添加的元素使用构造时候传入Comparator排序,要不然就使用元素的自然排序。
PriorityBlockingQueue是基于优先级,不是FIFO,这是个好东西,可以用来实现优先级的线程池,高优先级的先执行,低优先级的后执行。跟之前看过的几个队列一样,都是继承AbstractQueue实现BlockingQueue接口。
对于优先级的实现,是采用数组来实现堆的,大概样子画个图容易理解:
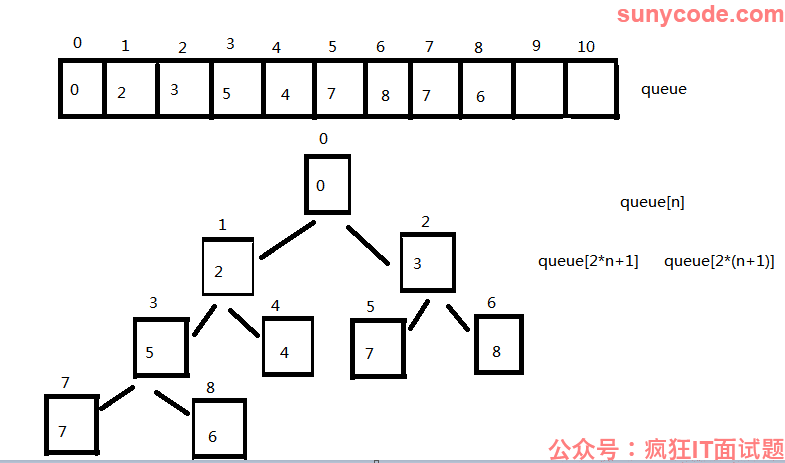
堆顶元素时最小的,对于各左右子堆也保证堆顶元素最小。
内部结构和构造:
//基于数组实现的,如果构造没有传入容量,就是用默认大小
private static final int DEFAULT_INITIAL_CAPACITY = 11;
/**
* 数组最大容量
*/
private static final int MAX_ARRAY_SIZE = Integer.MAX_VALUE - 8;
/**
* 优先级队列数组,记住queue[n]的2个左右子元素在数组的位置为在queue[2*n+1]和queue[2*(n+1)]
*/
private transient Object[] queue;
/**
* 队列元素个数
*/
private transient int size;
/**
* 比较器,构造时可以选择传入,没有就null,到时候就使用元素的自然排序
*/
private transient Comparator<? super E> comparator;
/**
* 重入锁控制多有操作
*/
private final ReentrantLock lock;
/**
* 队列为空的时候条件队列
*/
private final Condition notEmpty;
/**
* 自旋锁
*/
private transient volatile int allocationSpinLock;
/**
* 序列化的时候使用PriorityQueue,这个PriorityBlockingQueue几乎一模一样
*/
private PriorityQueue q;
/**
* 默认构造,使用默认容量,没有比较器
*/
public PriorityBlockingQueue() {
this(DEFAULT_INITIAL_CAPACITY, null);
}
public PriorityBlockingQueue(int initialCapacity) {
this(initialCapacity, null);
}
/**
* 最终调用的构造
*/
public PriorityBlockingQueue(int initialCapacity,
Comparator<? super E> comparator) {
if (initialCapacity < 1)
throw new IllegalArgumentException();
this.lock = new ReentrantLock();
this.notEmpty = lock.newCondition();
this.comparator = comparator;
this.queue = new Object[initialCapacity];
}
内部结构和构造没有什么特别的地方,基于数组实现优先级的堆,记住数组元素queue[n]的左节点queue[2*n+1]和右节点queue[2*(n+1)],每次出队的都是queue[0]。
看下常用方法:
add、put、offer都是最终调用offer()方法:
public boolean offer(E e) {
if (e == null)
throw new NullPointerException();
final ReentrantLock lock = this.lock;
lock.lock();
int n, cap;
Object[] array;
while ((n = size) >= (cap = (array = queue).length))
tryGrow(array, cap); //如果元素数量大于数组大小了,那就自动扩容,无界
try {
Comparator<? super E> cmp = comparator; //这个看构造的时候入参,没有就用自然排序
if (cmp == null)
siftUpComparable(n, e, array); //所有插入都用从底向上调整
else
siftUpUsingComparator(n, e, array, cmp);
size = n + 1;
notEmpty.signal(); //添加后通知非空条件队列可以take
} finally {
lock.unlock();
}
return true;
}
//数组扩容
private void tryGrow(Object[] array, int oldCap) {
lock.unlock(); // 数组扩容的时候使用自旋锁,不需要锁主锁,先释放
Object[] newArray = null;
if (allocationSpinLock == 0 &&
UNSAFE.compareAndSwapInt(this, allocationSpinLockOffset,
0, 1)) { //cas占用自旋锁
try {
int newCap = oldCap + ((oldCap < 64) ?
(oldCap + 2) : // grow faster if small
(oldCap >> 1)); //这里容量最少是翻倍
if (newCap - MAX_ARRAY_SIZE > 0) { // possible overflow
int minCap = oldCap + 1;
if (minCap < 0 || minCap > MAX_ARRAY_SIZE)
throw new OutOfMemoryError();
newCap = MAX_ARRAY_SIZE; //扩容后,默认最大
}
if (newCap > oldCap && queue == array)
newArray = new Object[newCap];
} finally {
allocationSpinLock = 0; //扩容后释放自旋锁
}
}
if (newArray == null) // 到这里如果是本线程扩容newArray肯定是不为null,为null就是其他线程在处理扩容,那就让给别的线程处理
Thread.yield();
lock.lock(); //这里重新重入锁,因为扩容后还有其他操作
if (newArray != null && queue == array) { //这里不为null那就复制数组
queue = newArray;
System.arraycopy(array, 0, newArray, 0, oldCap);
}
}
//所有插入都用从下向上调整
private static <T> void siftUpComparable(int k, T x, Object[] array) {
Comparable<? super T> key = (Comparable<? super T>) x;
while (k > 0) {
int parent = (k - 1) >>> 1; //取待插入节点的父节点
Object e = array[parent];
if (key.compareTo((T) e) >= 0) //如果比父节点大,那就无所谓退出,直接放在k位置
break;
array[k] = e; //比父节点小,按照k位置给父节点,然后从父节点开始继续向上查找
k = parent;
}
array[k] = key;
}
//所有插入都用从底向上调整,跟siftUpComparable方法类似就是比较的时候使用了构造传入的comparator
private static <T> void siftUpUsingComparator(int k, T x, Object[] array,
Comparator<? super T> cmp) {
while (k > 0) {
int parent = (k - 1) >>> 1;
Object e = array[parent];
if (cmp.compare(x, (T) e) >= 0)
break;
array[k] = e;
k = parent;
}
array[k] = x;
}
所有的添加元素最后都是调用offer方法,2步:扩容+存储,大体流程为:
1、 加锁,检查元素数量是否大于等于数组长度,如果是,那就扩容,扩容没必要使用主锁,先释放锁,使用cas自旋锁,容量最少翻倍,释放自旋锁,可能存在竞争,检查下,是否扩容,如果扩容那就复制数组,再度加主锁;
2、 看构造入参是否有comparator,有就使用,没有就自然排序,从数组待插入位置父节点开始比较大,如果大于父节点,那就直接待插入位置插入,否则就跟父节点交换,然后循环向上查找,数量加1,通知非空条件队列take,最后释放锁;
看下几个出队操作:
public E poll() {
final ReentrantLock lock = this.lock;
lock.lock();
try {
return dequeue();
} finally {
lock.unlock();
}
}
public E take() throws InterruptedException {
final ReentrantLock lock = this.lock;
lock.lockInterruptibly(); //响应中断
E result;
try {
while ( (result = dequeue()) == null)
notEmpty.await(); //如果take,数组没有元素是要阻塞的
} finally {
lock.unlock();
}
return result;
}
public E poll(long timeout, TimeUnit unit) throws InterruptedException {
long nanos = unit.toNanos(timeout);
final ReentrantLock lock = this.lock;
lock.lockInterruptibly(); //响应中断
E result;
try {
while ( (result = dequeue()) == null && nanos > 0)
nanos = notEmpty.awaitNanos(nanos); //响应超时,每次唤醒的超时时间要检查
} finally {
lock.unlock();
}
return result;
}
public E peek() {
final ReentrantLock lock = this.lock;
lock.lock();
try {
return (size == 0) ? null : (E) queue[0]; //只是获取元素,不移除
} finally {
lock.unlock();
}
}
//获取的基本都调用这个方法
private E dequeue() {
int n = size - 1;
if (n < 0)
return null;
else {
Object[] array = queue;
E result = (E) array[0];
E x = (E) array[n]; //将最后一个数组元素取出作为比较基准
array[n] = null; //出队,最后一个数组清掉,相当于堆的最底层最右的叶子节点清掉
Comparator<? super E> cmp = comparator;
if (cmp == null)
siftDownComparable(0, x, array, n); //从顶向下调整
else
siftDownUsingComparator(0, x, array, n, cmp);
size = n;
return result;
}
}
//从顶向下调整
private static <T> void siftDownComparable(int k, T x, Object[] array,
int n) {
if (n > 0) { //元素数量大于0,数组非空
Comparable<? super T> key = (Comparable<? super T>)x;
int half = n >>> 1; // 最后一个叶子节点的父节点位置
while (k < half) {
int child = (k << 1) + 1; // 待调整位置左节点位置
Object c = array[child]; //左节点
int right = child + 1; //右节点
if (right < n &&
((Comparable<? super T>) c).compareTo((T) array[right]) > 0)
c = array[child = right]; //左右节点比较,取小的
if (key.compareTo((T) c) <= 0) //如果待调整key最小,那就退出,直接赋值
break;
array[k] = c; //如果key不是最小,那就取左右节点小的那个放到调整位置,然后小的那个节点位置开始再继续调整
k = child;
}
array[k] = key;
}
}
出队的大体流程:
1、 加锁,获取queue[0],清掉堆的最后一个叶子节点,并将其作为比较节点;
2、 调用从顶向下调整的方法:待调整位置节点左右节点和之前的叶子节点比较,如果之前叶子节点最小,那就直接放入待调整位置,如果是叶子节点小,那就取小的那个放入待调整位置,并且将小的部分重新循环查找,循环次数根据2分查找,基本是元素数量的一半就到找到位置;
再看一个remove,因为remove方法,2中调整方式都用到了:
public boolean remove(Object o) {
final ReentrantLock lock = this.lock;
lock.lock();
try {
int i = indexOf(o); //查找o在数组中位置
if (i == -1)
return false;
removeAt(i); //remove掉
return true;
} finally {
lock.unlock();
}
}
//o在数组中的位置
private int indexOf(Object o) {
if (o != null) {
Object[] array = queue;
int n = size;
for (int i = 0; i < n; i++)
if (o.equals(array[i]))
return i;
}
return -1;
}
//remove掉数组指定位置的元素
//跟之前take的dequeue相似的地方,dequeue是remove掉0的位置,然后调整也是从0的位置开始调整,这里是从指定位置调整
private void removeAt(int i) {
Object[] array = queue;
int n = size - 1;
if (n == i) // removed last element
array[i] = null;
else {
E moved = (E) array[n]; //跟dequeue一样也是最后一个叶子节点作为比较
array[n] = null;
Comparator<? super E> cmp = comparator;
if (cmp == null)
siftDownComparable(i, moved, array, n); //从指定位置调整
else
siftDownUsingComparator(i, moved, array, n, cmp);
//经过从上向下调整后,如果是直接将比较节点放在待调整位置,那只能说明这个节点在以它为堆顶的堆里面最小,但不能说明从这个节点就向上查找就最大
//这里需要自底向上再来一次调整
if (array[i] == moved) {
if (cmp == null)
siftUpComparable(i, moved, array);
else
siftUpUsingComparator(i, moved, array, cmp);
}
}
size = n;
}
remove的时候有2个调整,先自顶向下调整,保证最小,然后再向上调整。
其他的方法不看了,都这个意思。
为了我的目标继续学习,生命不止,学习不止。