13、数据结构与算法 - 实战:树
0. 遍历二叉树
方式
前序遍历:根 → 左子树 → 右子树
中序遍历:左子树 → 根 → 右子树
后序遍历:左子数 → 右子树 → 根
层次遍历:顶层开始琢层进行遍历,每层从左到右遍历

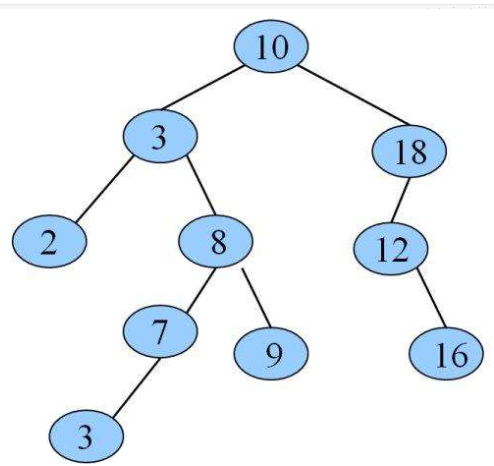
图中的完全二叉树四大遍历形式的结果:
1、 *前序遍历:*93046584979;
2、 *中序遍历:*46305897949;
3、 *后续遍历:*46583079499;
4、 *层次遍历:*93049465879;
1. 基本类 - Student、TreeEnumeration
Student.java
public class Student {
Integer id;
String name;
Integer year;
public Student() {
}
public Student(Integer id, String name, Integer year) {
this.id = id;
this.name = name;
this.year = year;
}
public Integer getId() {
return id;
}
public void setId(Integer id) {
this.id = id;
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
public Integer getYear() {
return year;
}
public void setYear(Integer year) {
this.year = year;
}
@Override
public String toString() {
return "Student{" +
"id=" + id +
", name='" + name + '\'' +
'}';
}
public static void main(String[] args) throws Exception {
OrderType orderType = null;
orderType = OrderType.POST_ORDER;
switch(orderType) {
case POST_ORDER:
System.out.println(1);
}
}
}
TreeEnumeration.java
public enum TreeEnumeration {
POST_ORDER, IN_ORDER, PRE_ORDER, POST_CLUE_ORDER,IN_CLUE_ORDER, PRE_CLUE_ORDER,
POST_SEARCH, IN_SEARCH, PRE_SEARCH,
REMOVE_SON_TREE, REMOVE_SINGLE_NODE,
PRE_ORDER_CLUE, IN_ORDER_CLUE, POST_ORDER_CLUE
}
2. 二叉排序(查找)树
满足下列条件 - (中序遍历元素是升序排列)
1、 左节点小于父节点;
2、 右节点大于父节点;
3、 所有节点的左右子树都需满足1、2条件;
BinarySortTree.java
/**
* @Classname BinarySortTree
* @Description
* @Date 2022/4/11 23:50
* @Created by lrc
*/
public class BinarySortTree<T> {
Node<T> root;
private Integer curNodeNum = 0;
private List<T> orderList;
//二叉树构造函数
BinarySortTree(T... datas) {
for(T data: datas ) {
add(data);
}
}
//添加二叉树节点
public boolean add(T data) {
Node<T> newNode = new Node<T>();
newNode.setData(data);
if(root == null) {
root = newNode;
}else {
Node<T> curNode = root;
Integer newId = newNode.getId();
//添加节点阶段
while(true) {
// 获取当前遍历到的节点的ID号
Integer curId = curNode.getId();
// 如果添加节点ID号与当前节点ID号小,则当前节点的左子节点进行遍历
if(newId < curId) {
if(curNode.getLeftNode() == null) {
curNode.setLeftNode(newNode);
break;
}
curNode = curNode.getLeftNode();
// 如果添加节点ID号与当前节点ID号大,则当前节点的右子节点进行遍历
}else if(newId > curId) {
if(curNode.getRightNode() == null) {
curNode.setRightNode(newNode);
break;
}
curNode = curNode.getRightNode();
//如果添加节点ID号与当前节点ID号等于,则直接抛出异常
}else {
throw new RuntimeException("不可添加重复ID号的节点");
}
}
}
++this.curNodeNum;
return true;
}
//前序遍历
private void preOrder(Node<T> node) {
if(node != null ) {
orderList.add(node.getData());
}
if(node.leftNode != null) {
preOrder(node.getLeftNode());
}
if(node.rightNode != null) {
preOrder(node.getRightNode());
}
}
//中序遍历
private void inOrder(Node<T> node) {
if(node != null ) {
if(node.getLeftNode() != null) {
inOrder(node.getLeftNode());
}
orderList.add(node.getData());
if(node.getRightNode() != null) {
inOrder(node.getRightNode());
}
}
}
//后序遍历
private void postOrder(Node<T> node) {
if(node != null ) {
if(node.getLeftNode() != null) {
postOrder(node.getLeftNode());
}
if(node.getRightNode() != null) {
postOrder(node.getRightNode());
}
orderList.add(node.getData());
}
}
// 遍历树
public List<T> order(TreeEnumeration treeEnumeration) {
if(orderList == null) {
orderList = new ArrayList<>(curNodeNum);
}else {
orderList.clear();
}
switch (treeEnumeration) {
case PRE_ORDER: {
preOrder(root);break;}
case IN_ORDER: {
inOrder(root);break;}
case POST_ORDER: {
postOrder(root);break;}
default: throw new RuntimeException("请输入合法的排序枚举常量");
}
return orderList;
}
//前序遍历查找
public T preOrderSearch(Node<T> node, int id) {
T t = null;
if(node != null) {
Integer curId = node.getId();
if(curId == id) {
t = node.getData();
}else if( node.getLeftNode() != null && curId > id ){
t = preOrderSearch(node.getLeftNode(), id);
}else if(node.getRightNode() != null && curId < id) {
t = preOrderSearch(node.getRightNode(), id);
}
}
return t;
}
//中序遍历查找
public T inOrderSearch(Node<T> node, int id) {
T t = null;
if(node != null) {
Integer curId = node.getId();
if(node.getLeftNode() != null && curId > id) {
t = preOrderSearch(node.getLeftNode(), id);
}else if( curId == id ){
t = node.getData();
}else if(node.getRightNode() != null && curId < id) {
t = preOrderSearch(node.getRightNode(), id);
}
}
return t;
}
//后序遍历查找
public T postOrderSearch(Node<T> node, int id) {
T t = null;
if(node != null) {
Integer curId = node.getId();
if(node.getLeftNode() != null && curId > id) {
t = preOrderSearch(node.getLeftNode(), id);
}else if(node.getRightNode() != null && curId < id) {
t = preOrderSearch(node.getRightNode(), id);
}else if( curId == id ){
t = node.getData();
}
}
return t;
}
// 遍历树通过ID号查找元素并返回 -
public T search(int id, TreeEnumeration treeEnumeration) {
T t = null;
switch (treeEnumeration) {
case PRE_SEARCH: {
t = preOrderSearch(root,id);break;}
case IN_SEARCH: {
t = inOrderSearch(root,id);break;}
case POST_SEARCH: {
t = postOrderSearch(root,id);break;}
default: throw new RuntimeException("请输入合法的查找枚举常量");
}
return t;
}
//把当前子树一同删除,而不是单纯只删一个节点
private boolean removeSonTree(int id) {
boolean isDeleted = false;
if(root == null) {
isDeleted = false;
}else {
Node<T> fatherNode = null;
Node<T> curNode = root;
while(true) {
Integer curId = curNode.getId();
//当前节点
if(curId == id) {
if(fatherNode == null) {
root = null;
}else {
if(fatherNode.getLeftNode() == curNode) {
fatherNode.setLeftNode(null);
}
if(fatherNode.getRightNode() == curNode) {
fatherNode.setRightNode(null);
}
}
isDeleted = true;
break;
}
Node<T> nextNode;
//左节点
if(curId < id) {
nextNode = curNode.getRightNode();
if(nextNode == null) {
break;
}
fatherNode = curNode;
curNode = nextNode;
}
//右节点
if(curId > id) {
nextNode = curNode.getLeftNode();
if(nextNode == null) {
break;
}
fatherNode = curNode;
curNode = nextNode;
}
}
}
return isDeleted;
}
//只删除当前节点 - 优先左节点代替被删除节点
private boolean removeSignleNode(int id) {
boolean isDeleted = false;
if(root == null) {
isDeleted = false;
}else {
Node<T> fatherNode = null;
Node<T> curNode = root;
while(true) {
Integer curId = curNode.getId();
//当前节点
if(curId == id) {
if(fatherNode == null) {
root = null;
}else {
//标记删除的节点是父节点的左节点还是右节点 0左节点 1右节点
int flagLeftOrRight = 0;
if(fatherNode.getLeftNode() == curNode) {
fatherNode.setLeftNode(null);
flagLeftOrRight = 0;
}
if(fatherNode.getRightNode() == curNode) {
fatherNode.setRightNode(null);
flagLeftOrRight = 1;
}
//将取代被删除节点的节点
Node<T> replaceDeleteNode;
//遍历curNode右节点的节点
Node<T> traverseNode;
replaceDeleteNode = curNode.getLeftNode();
//当前节点存在左节点
if(replaceDeleteNode != null) {
if(flagLeftOrRight == 0) {
fatherNode.leftNode = replaceDeleteNode;
}else {
fatherNode.rightNode = replaceDeleteNode;
}
当前节点存在右节点
if(curNode.getRightNode() != null) {
traverseNode = curNode;
while(true) {
if(traverseNode.getRightNode() == null) {
traverseNode.setRightNode(curNode.getRightNode());
break;
}
traverseNode = traverseNode.getRightNode();
}
}
}else {
replaceDeleteNode = curNode.getRightNode();
if(flagLeftOrRight == 0) {
fatherNode.leftNode = replaceDeleteNode;
}else {
fatherNode.rightNode = replaceDeleteNode;
}
}
}
isDeleted = true;
break;
}
Node<T> nextNode;
//左节点
if(curId < id) {
nextNode = curNode.getRightNode();
if(nextNode == null) {
break;
}
fatherNode = curNode;
curNode = nextNode;
}
//右节点
if(curId > id) {
nextNode = curNode.getLeftNode();
if(nextNode == null) {
break;
}
fatherNode = curNode;
curNode = nextNode;
}
}
}
return isDeleted;
}
public boolean remove(int id, TreeEnumeration treeEnumeration) {
boolean flag =false;
switch(treeEnumeration) {
case REMOVE_SON_TREE: {
flag = removeSonTree(id);break;}
case REMOVE_SINGLE_NODE: {
flag = removeSignleNode(id);break;}
default:new RuntimeException("请输入合法的删除操作");
}
return flag;
}
// 重写toString方法 -其实就是中序遍历输出
@Override
public String toString() {
order(TreeEnumeration.IN_ORDER);
return orderList.toString();
}
private class Node<T> {
T data;
Node<T> leftNode;
Node<T> rightNode;
public Integer getId() {
Integer id = null;
try {
Field field = data.getClass().getDeclaredField("id");
field.setAccessible(true);
id = (Integer) field.get(data);
}catch(Exception e) {
e.printStackTrace();
}
return id;
}
public T getData() {
return data;
}
public void setData(T data) {
this.data = data;
}
public Node<T> getLeftNode() {
return leftNode;
}
public void setLeftNode(Node<T> leftNode) {
this.leftNode = leftNode;
}
public Node<T> getRightNode() {
return rightNode;
}
public void setRightNode(Node<T> rightNode) {
this.rightNode = rightNode;
}
}
public static void main(String[] args) {
//数据准备
Student student1 = new Student(1, "lrc", 23);
Student student2 = new Student(2, "tyr", 21);
Student student3 = new Student(3, "smis", 30);
Student student4 = new Student(4, "tony", 43);
Student student5 = new Student(5, "ghy", 18);
Student student6 = new Student(5, "ghy", 18);
Student student7 = new Student(7, "ert", 35);
Student[] students1 = {
student3,student1,student2,student4,student5};
Student[] students2 = {
student3,student1,student2,student4,student5,student6};
//构造二叉排序树1
BinarySortTree<Student> tree1 = new BinarySortTree<>(students1);
System.out.printf("tree1前序遍历:%s\n",tree1.order(TreeEnumeration.PRE_ORDER));
System.out.printf("tree1中序遍历:%s\n",tree1.order(TreeEnumeration.IN_ORDER));
System.out.printf("tree1后序遍历:%s\n\n",tree1.order(TreeEnumeration.POST_ORDER));
tree1.add(student7);
System.out.printf("tree1添加节点后前序遍历:%s\n",tree1.order(TreeEnumeration.PRE_ORDER));
System.out.printf("tree1添加节点后中序遍历:%s\n",tree1.order(TreeEnumeration.IN_ORDER));
System.out.printf("tree1添加节点后后序遍历:%s\n\n",tree1.order(TreeEnumeration.POST_ORDER));
Student searchStu = null;
searchStu = tree1.search(4, TreeEnumeration.PRE_SEARCH);
System.out.printf("Tree1前序遍历查找ID为4的节点:%s\n", searchStu);
searchStu = tree1.search(4, TreeEnumeration.IN_SEARCH);
System.out.printf("Tree1中序遍历查找ID为4的节点:%s\n", searchStu);
searchStu = tree1.search(4, TreeEnumeration.POST_SEARCH);
System.out.printf("Tree1后序遍历查找ID为4的节点:%s\n\n", searchStu);
tree1.remove(4, TreeEnumeration.REMOVE_SINGLE_NODE);
System.out.printf("Tree1仅删除ID为4的节点后前序遍历:%s\n",tree1.order(TreeEnumeration.PRE_ORDER));
tree1.add(student4);
System.out.printf("Tree1添加ID为4的节点后前序遍历:%s\n",tree1.order(TreeEnumeration.PRE_ORDER));
tree1.remove(4, TreeEnumeration.REMOVE_SON_TREE);
System.out.printf("Tree1删除以ID为4的根节点的子树后前序遍历:%s\n\n", tree1.order(TreeEnumeration.IN_ORDER));
//构造二叉排序树2 - 构造异常,因为有相同ID号
BinarySortTree<Student> tree2 = new BinarySortTree<>(students2);
}
}
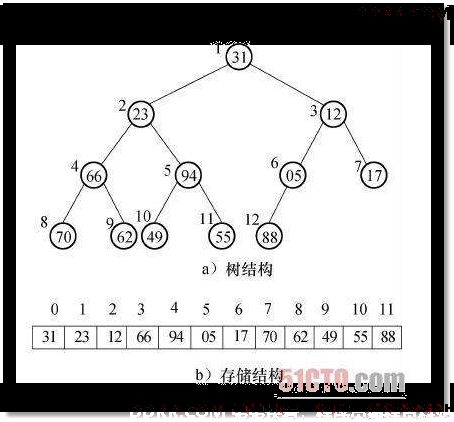
3. 顺序存储二叉树 - 完全二叉树结构
特点:N从0开始
- 第N个数组索引的左节点的数组索引是:2 * N + 1
- 第N个数组索引的右节点的数组索引是:2 * N + 2
- 第N个数组索引的父节点的数组索引是:(N-1)/2
SequentialStorageTree.java
/**
* @Classname SequentialStorageTree
* @Description
* @Date 2022/4/12 13:32
* @Created by lrc
*/
public class SequentialStorageTree<T> {
private T[] datas;
private StringBuilder orderStr = new StringBuilder();
SequentialStorageTree(T... datas) {
this.datas = datas;
}
//遍历顺序存储树
public String order(TreeEnumeration treeEnumeration) {
//清空之前的遍历结果
orderStr.delete(0,orderStr.length());
orderStr.append("[");
switch(treeEnumeration) {
case PRE_ORDER: {
preOrder(0); break;}
case IN_ORDER:{
inOrder(0); break;}
case POST_ORDER: {
postOrder(0); break;}
default: new RuntimeException("请输入合法的排序枚举常量");
}
orderStr.replace(orderStr.lastIndexOf(", "), orderStr.length(), "");
orderStr.append("]");
return orderStr.toString();
}
//递归 - 前序遍历通过index进行查询节点
public void preOrder(int index) {
if(index < datas.length && datas[index] != null) {
orderStr.append(datas[index] + ", ");
}
int nextIndex = 2*index + 1;
if(nextIndex < datas.length) {
preOrder(nextIndex);
}
nextIndex = 2*index + 2;
if(nextIndex < datas.length) {
preOrder(nextIndex);
}
}
//递归 - 中序遍历通过index进行查询节点
public void inOrder(int index) {
int nextIndex = 2*index + 1;
if(nextIndex < datas.length) {
inOrder(nextIndex);
}
if(index < datas.length && datas[index] != null) {
orderStr.append(datas[index] + ", ");
}
nextIndex = 2*index + 2;
if(nextIndex < datas.length) {
inOrder(nextIndex);
}
}
//递归 - 中序遍历通过index进行查询节点
public void postOrder(int index) {
int nextIndex = 2*index + 1;
if(nextIndex < datas.length) {
postOrder(nextIndex);
}
nextIndex = 2*index + 2;
if(nextIndex < datas.length) {
postOrder(nextIndex);
}
if(index < datas.length && datas[index] != null) {
orderStr.append(datas[index] + ", ");
}
}
public static void main(String[] args) {
//数据准备
Student student1 = new Student(1, "lrc", 23);
Student student2 = new Student(2, "tyr", 21);
Student student3 = new Student(3, "smis", 30);
Student student4 = new Student(4, "tony", 43);
Student student5 = new Student(5, "ghy", 18);
Student[] students1 = {
student3,student1,student2,student4,student5};
SequentialStorageTree<Student> tree = new SequentialStorageTree(students1);
System.out.printf("前序遍历:%s\n" ,tree.order(TreeEnumeration.PRE_ORDER));
System.out.printf("中序遍历:%s\n" ,tree.order(TreeEnumeration.IN_ORDER));
System.out.printf("后序遍历:%s\n" ,tree.order(TreeEnumeration.POST_ORDER));
}
}

4. 线索化二叉排序树
思路:将二叉排序树的Null左右指针利用起来
指针
左Null指针:前驱节点指针
右Null指针:后继节点指针
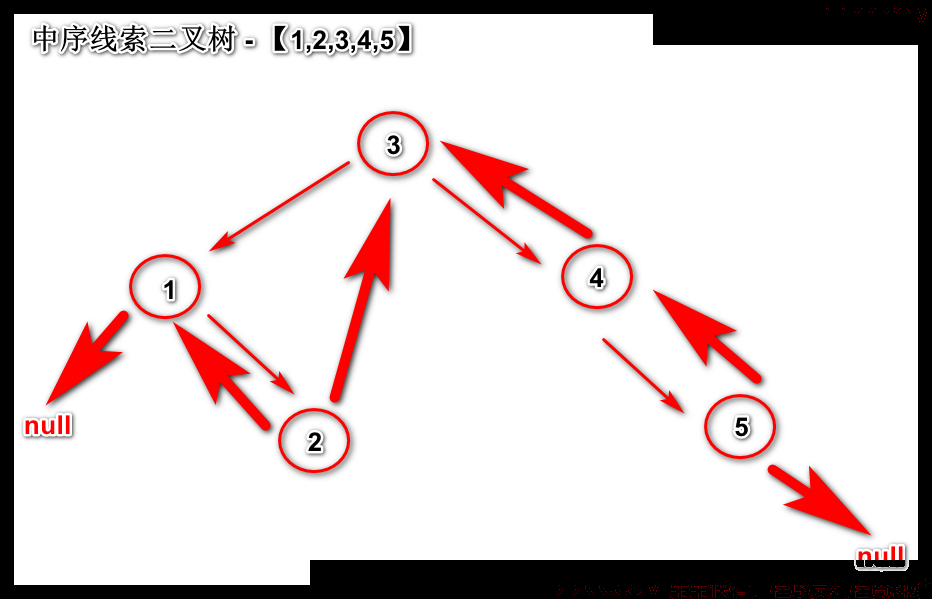
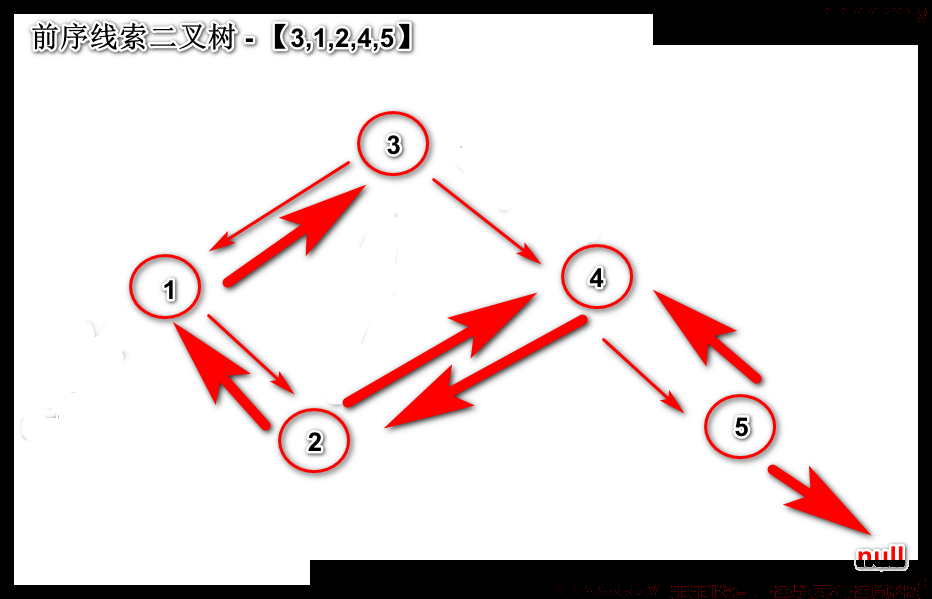
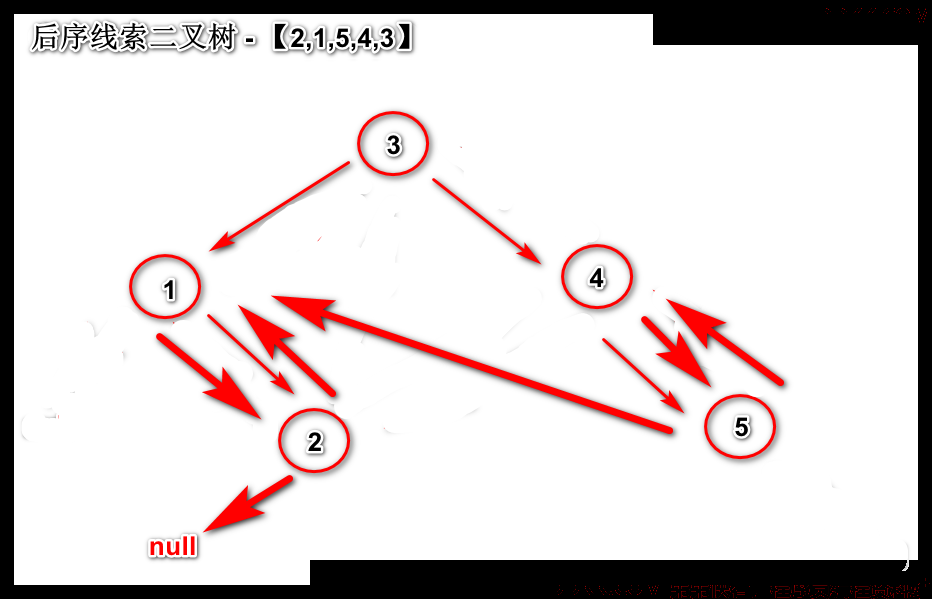
线索化二叉排序树
前序线索二叉树
中序线索二叉树
后序线索二叉树
粗的箭头线即是线索
ThreadedBinaryTree.java
/**
* @Classname ThreadedBinaryTree
* @Description
* @Date 2022/4/12 15:42
* @Created by lrc
*/
public class ThreadedBinaryTree<T> {
Node<T> root;
//当前遍历接节点的前驱节点
Node<T> pre = null;
private Integer curNodeNum = 0;
private List<T> orderList;
//二叉树构造函数 - 默认前序线索二叉树
ThreadedBinaryTree(T... datas) {
for (T data : datas) {
add(data);
}
clues(TreeEnumeration.PRE_ORDER_CLUE);
}
public static void main(String[] args) {
//数据准备
Student student1 = new Student(1, "lrc", 23);
Student student2 = new Student(2, "tyr", 21);
Student student3 = new Student(3, "smis", 30);
Student student4 = new Student(4, "tony", 43);
Student student5 = new Student(5, "ghy", 18);
Student[] students = {
student3, student1, student2, student4, student5};
//前序线索二叉排序树
ThreadedBinaryTree<Student> tree = new ThreadedBinaryTree<>(students);
//前序线索二叉排序树 - 前序、中序、后序遍历 - 不依赖线索
System.out.println("\n前序线索二叉排序树 - 前序、中序、后序遍历 - 不依赖线索------------------");
System.out.println(tree.order(TreeEnumeration.PRE_ORDER));
System.out.println(tree.order(TreeEnumeration.IN_ORDER));
System.out.println(tree.order(TreeEnumeration.POST_ORDER));
//寻找id为2、3的元素
System.out.println("\n寻找元素--------------------");
System.out.println(tree.preOrderSearch(2));
System.out.println(tree.preOrderSearch(3));
//修改二叉树的排序线索时,必须先清空原来的线索
tree.clearClues();
System.out.println("\n中序线索二叉排序树 - 依赖线索遍历以及节点的信息----------------------");
tree.clues(TreeEnumeration.IN_ORDER_CLUE);
System.out.println(tree.order(TreeEnumeration.IN_CLUE_ORDER));
System.out.println(tree.preOrderSearch(1));
System.out.println(tree.preOrderSearch(2));
System.out.println(tree.preOrderSearch(4));
System.out.println(tree.preOrderSearch(5));
tree.clearClues();
System.out.println("\n后序线索二叉排序树 - 依赖线索遍历以及节点的信息----------------------");
tree.clues(TreeEnumeration.POST_ORDER_CLUE);
System.out.println(tree.order(TreeEnumeration.POST_CLUE_ORDER));
System.out.println(tree.preOrderSearch(1));
System.out.println(tree.preOrderSearch(2));
System.out.println(tree.preOrderSearch(4));
System.out.println(tree.preOrderSearch(5));
tree.clearClues();
System.out.println("\n前序线索二叉排序树 - 依赖线索遍历以及节点的信息----------------------");
tree.clues(TreeEnumeration.PRE_ORDER_CLUE);
System.out.println(tree.order(TreeEnumeration.PRE_CLUE_ORDER));
System.out.println(tree.preOrderSearch(1));
System.out.println(tree.preOrderSearch(2));
System.out.println(tree.preOrderSearch(4));
System.out.println(tree.preOrderSearch(5));
}
//添加二叉树节点
public boolean add(T data) {
Node<T> newNode = new Node<T>();
newNode.setData(data);
if (root == null) {
root = newNode;
} else {
Node<T> curNode = root;
Integer newId = newNode.getId();
//添加节点阶段
while (true) {
// 获取当前遍历到的节点的ID号
Integer curId = curNode.getId();
// 如果添加节点ID号与当前节点ID号小,则当前节点的左子节点进行遍历
if (newId < curId) {
if (curNode.getLeftNode() == null) {
curNode.setLeftNode(newNode);
break;
}
curNode = curNode.getLeftNode();
// 如果添加节点ID号与当前节点ID号大,则当前节点的右子节点进行遍历
} else if (newId > curId) {
if (curNode.getRightNode() == null) {
curNode.setRightNode(newNode);
break;
}
curNode = curNode.getRightNode();
//如果添加节点ID号与当前节点ID号等于,则直接抛出异常
} else {
throw new RuntimeException("不可添加重复ID号的节点");
}
}
}
++this.curNodeNum;
return true;
}
//前序遍历
private void preOrder(Node<T> node) {
if (node != null) {
orderList.add(node.getData());
}
if (node.leftNode != null && node.flagLeftNode == 0) {
preOrder(node.getLeftNode());
}
if (node.rightNode != null && node.flagRightNode == 0) {
preOrder(node.getRightNode());
}
}
//中序遍历
private void inOrder(Node<T> node) {
if (node != null) {
if (node.getLeftNode() != null && node.flagLeftNode == 0) {
inOrder(node.getLeftNode());
}
orderList.add(node.getData());
if (node.getRightNode() != null && node.flagRightNode == 0) {
inOrder(node.getRightNode());
}
}
}
//中序线索遍历
private void inClueOrder() {
Node<T> curNode = root;
while (curNode != null) {
//先找最左节点
while (curNode.flagLeftNode == 0) {
curNode = curNode.leftNode;
}
orderList.add(curNode.getData());
//根据线索找到下一个节点
while (curNode.flagRightNode == 1) {
curNode = curNode.rightNode;
orderList.add(curNode.getData());
}
curNode = curNode.rightNode;
}
}
//前序线索遍历
private void preClueOrder() {
Node<T> curNode = root;
while (curNode != null) {
//一来就直接读取
orderList.add(curNode.getData());
//根据线索找到下一个节点
while (curNode.flagRightNode == 1) {
if (curNode.rightNode == null) {
break;
}
curNode = curNode.rightNode;
orderList.add(curNode.getData());
}
while (curNode.flagLeftNode == 0) {
curNode = curNode.leftNode;
orderList.add(curNode.getData());
}
curNode = curNode.rightNode;
}
}
//后序线索遍历
private void postClueOrder() {
Node<T> curNode = root;
//判断是否有遍历根节点的右子树
boolean flag = false;
//循环
while(curNode != null) {
//找最左节点
while (curNode.flagLeftNode == 0 && curNode.leftNode != null) {
curNode = curNode.leftNode;
}
//如果当前节点含有右节点 - 则说明还不是最左节点
if(curNode.rightNode != null && curNode.flagRightNode == 0) {
curNode = curNode.rightNode;
continue;
}
//已经判断了这肯定是最左节点 - 故添加
orderList.add(curNode.getData());
//根据线索找到下一个节点
while (curNode.flagRightNode == 1) {
curNode = curNode.rightNode;
orderList.add(curNode.getData());
//如果刚好有线索到根节点 -- 添加完直接退出遍历即可
if(curNode == root) {
return;
}
}
//已经遍历完右节点,然而还是没有线索到根节点 - 只能手动添加根节点信息
if(flag) {
orderList.add(root.getData());
break;
}
curNode = root.rightNode;
//准备遍历根节点的右子树
flag = true;
}
}
//后序遍历
private void postOrder(Node<T> node) {
if (node != null) {
if (node.getLeftNode() != null && node.flagLeftNode == 0) {
postOrder(node.getLeftNode());
}
if (node.getRightNode() != null && node.flagRightNode == 0) {
postOrder(node.getRightNode());
}
orderList.add(node.getData());
}
}
// 遍历树
public List<T> order(TreeEnumeration treeEnumeration) {
if (orderList == null) {
orderList = new ArrayList<>(curNodeNum);
} else {
orderList.clear();
}
switch (treeEnumeration) {
case PRE_ORDER: {
preOrder(root);
break;
}
case IN_ORDER: {
inOrder(root);
break;
}
case POST_ORDER: {
postOrder(root);
break;
}
case PRE_CLUE_ORDER: {
preClueOrder();
break;
}
case IN_CLUE_ORDER: {
inClueOrder();
break;
}
case POST_CLUE_ORDER: {
postClueOrder();
break;
}
default:
throw new RuntimeException("请输入合法的排序枚举常量");
}
return orderList;
}
//前序遍历查找
private Node<T> preOrderSearch(Node<T> node, int id) {
Node<T> resultNode = null;
if (node != null) {
Integer curId = node.getId();
if (curId == id) {
resultNode = node;
} else if (node.getLeftNode() != null && curId > id && node.flagLeftNode != 1) {
resultNode = preOrderSearch(node.getLeftNode(), id);
} else if (node.getRightNode() != null && curId < id && node.flagRightNode != 1) {
resultNode = preOrderSearch(node.getRightNode(), id);
}
}
return resultNode;
}
public Node<T> preOrderSearch(int id) {
return preOrderSearch(root, id);
}
//把排序树的所有线索去掉,返回原来的普通二叉排序树
public boolean clearClues() {
if (root != null) {
root.clearClue(root);
return true;
} else {
return false;
}
}
//给二叉排序树进行添加线索 - 前序、后序、中序
private void clues(TreeEnumeration treeEnumeration) {
switch (treeEnumeration) {
//pre.flagRightNode = 1;这句话特别关键,因为在节点中后继节点的更改需要等下一个元素进行变更
case PRE_ORDER_CLUE: {
root.preClues(root);
pre.flagRightNode = 1;
break;
}
case IN_ORDER_CLUE: {
root.inClues(root);
break;
}
case POST_ORDER_CLUE: {
root.postClues(root);
break;
}
default:
throw new RuntimeException("请选择合适的树线索");
}
//将pre置空
pre = null;
}
// 重写toString方法 -其实就是中序遍历输出
@Override
public String toString() {
order(TreeEnumeration.IN_ORDER);
return orderList.toString();
}
private class Node<T> {
T data;
Node<T> leftNode;
Node<T> rightNode;
//用于标记左节点是子树还是前驱节点 - 0表示是子树 1表示前驱节点
int flagLeftNode = 0;
//用于标记右节点是子树还是后继节点 - 0表示是子树 1表示后继节点
int flagRightNode = 0;
private void clearClue(Node<T> node) {
if (node.flagLeftNode == 1) {
node.leftNode = null;
node.flagLeftNode = 0;
}
if (node.flagRightNode == 1) {
node.rightNode = null;
node.flagRightNode = 0;
}
if (node.leftNode != null) {
clearClue(node.leftNode);
}
if (node.rightNode != null) {
clearClue(node.rightNode);
}
}
private void inClues(Node node) {
if (node == null) {
return;
}
//1. 线索左节点
inClues(node.leftNode);
//2. 线索当前节点
//2.1 前驱节点
if (node.leftNode == null && node.flagLeftNode == 0) {
node.flagLeftNode = 1;
node.leftNode = ThreadedBinaryTree.this.pre;
}
//2.2 后继节点
if (pre != null && pre.rightNode == null) {
pre.rightNode = node;
pre.flagRightNode = 1;
}
//改变前驱节点
ThreadedBinaryTree.this.pre = node;
//3.线索右节点
inClues(node.rightNode);
}
private void preClues(Node node) {
if (node == null) {
return;
}
Node curPre = ThreadedBinaryTree.this.pre;
//1. 线索当前节点
//1.1 前驱节点
if (node.leftNode == null && node.flagLeftNode == 0) {
node.flagLeftNode = 1;
node.leftNode = ThreadedBinaryTree.this.pre;
}
//1.2 后继节点
if (pre != null && pre.rightNode == null) {
pre.rightNode = node;
pre.flagRightNode = 1;
}
//改变前驱节点
ThreadedBinaryTree.this.pre = node;
//2. 线索左节点
inClues(node.leftNode);
//3.线索右节点
inClues(node.rightNode);
}
private void postClues(Node node) {
if (node == null) {
return;
}
//1. 线索左节点
postClues(node.leftNode);
//2.线索右节点
postClues(node.rightNode);
//3. 线索当前节点
//3.1 前驱节点
if (node.leftNode == null && node.flagLeftNode == 0) {
node.flagLeftNode = 1;
node.leftNode = ThreadedBinaryTree.this.pre;
}
//3.2 后继节点
if (pre != null && pre.rightNode == null) {
pre.rightNode = node;
pre.flagRightNode = 1;
}
//改变前驱节点
ThreadedBinaryTree.this.pre = node;
}
public Integer getId() {
Integer id = null;
try {
Field field = data.getClass().getDeclaredField("id");
field.setAccessible(true);
id = (Integer) field.get(data);
} catch (Exception e) {
e.printStackTrace();
}
return id;
}
public T getData() {
return data;
}
public void setData(T data) {
this.data = data;
}
public Node<T> getLeftNode() {
return leftNode;
}
public void setLeftNode(Node<T> leftNode) {
this.leftNode = leftNode;
}
public Node<T> getRightNode() {
return rightNode;
}
public void setRightNode(Node<T> rightNode) {
this.rightNode = rightNode;
}
//重写Node的toString方法 - 目的方便查看node内部变化
@Override
public String toString() {
return "Node{" +
"data=" + data +
", leftNode=" + (leftNode == null ? null : leftNode.getData()) +
", rightNode=" + (rightNode == null ? null : rightNode.getData()) +
", flagLeftNode=" + (flagLeftNode == 0 ? "普通左子树节点" : "前驱节点指针") +
", flagRightNode=" + (flagRightNode == 0 ? "普通右子树节点" : "后继节点指针") +
'}';
}
}
}

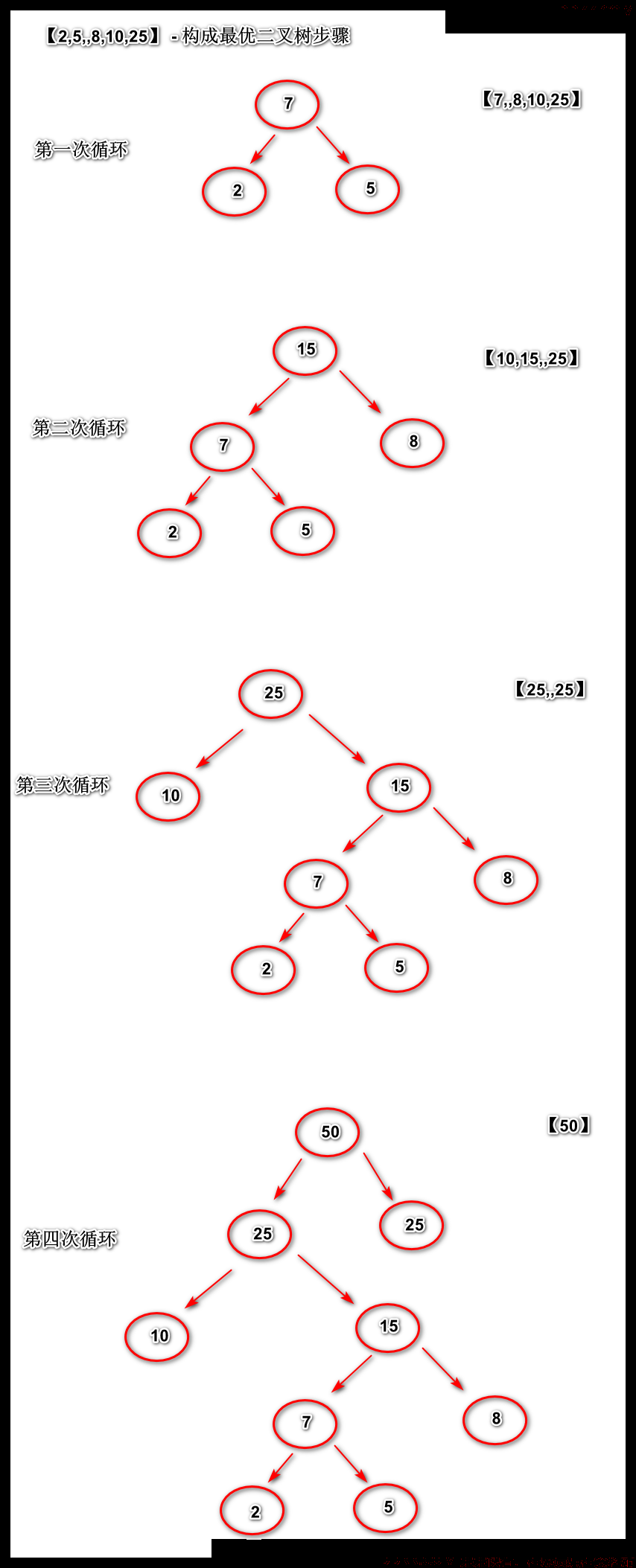
5. 最优二叉(赫夫曼)树
叶子结点的带权路径长度和最小的二叉树
- 思路
1、 数组元素是升序排序;
2、 从数组中弹出两个元素构成一个3节点的二叉树(这两个元素是叶子节点);
3、 将根节点(步骤2的叶子节点权值和)的权值加入到数组中,并再次升序数组;
4、 重复1,2,3直到数组中只有一个元素就停止循环;
流程图
Student.java
/**
* @Classname Student
* @Description
* @Date 2022/4/11 19:21
* @Created by lrc
*/
public class Student implements Comparable<Student> {
Integer id;
String name;
Integer year;
Integer weight;
public Student() {
}
public Student(Integer id, String name, Integer year) {
this.id = id;
this.name = name;
this.year = year;
this.weight = year;
}
public Integer getId() {
return id;
}
public void setId(Integer id) {
this.id = id;
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
public Integer getYear() {
return year;
}
public void setYear(Integer year) {
this.year = year;
this.weight = year;
}
@Override
public String toString() {
return "Student{" +
"id=" + id +
", name='" + name + '\'' +
", year=" + year +
'}';
}
@Override
public int compareTo(Student stu) {
Integer curYear = this.getYear();
Integer comapareYear = stu.getYear();
if(curYear > comapareYear) {
return 1;
}else if (curYear < comapareYear) {
return -1;
}else {
return 0;
}
}
}
OptimalBinaryTree.java
public class OptimalBinaryTree<T> {
//二叉树根节点 - 根据datas进行组建
Node<T> root;
//构造器传入的数据
T[] datas;
//传数组构造最优二叉树
OptimalBinaryTree(T...datas) {
T[] copyData = Arrays.copyOf(datas, datas.length);
Arrays.sort(copyData);
datas = copyData;
createdOptimalBinaryTree(datas);
}
// 最优二叉树 - 中序遍历
public String inOrder() {
StringBuilder sb = new StringBuilder();
sb.append("[");
//真正的中序遍历
root.inOrder(root,sb);
sb.replace(sb.lastIndexOf(", "), sb.length(), "");
sb.append("]");
return sb.toString();
}
// 最优二叉树 - 前序遍历
public String preOrder() {
StringBuilder sb = new StringBuilder();
sb.append("[");
//真正的前序遍历
root.preOrder(root,sb);
sb.replace(sb.lastIndexOf(", "), sb.length(), "");
sb.append("]");
return sb.toString();
}
@Override
public String toString() {
return preOrder();
}
private boolean createdOptimalBinaryTree(T[] datas) {
LinkedList<Node<T>> list = new LinkedList<>();
boolean flag = false;
Node<T> newNode;
for(T data : datas) {
newNode = new Node<>();
newNode.setData(data);
list.add( newNode );
}
while(true) {
//弹出两个子节点,构成左右子树
Node<T> lNode = list.pop();
Node<T> rNode = list.pop();
//父节点权重是上面两个子节点的权重
Node<T> parNode = new Node<>();
parNode.weight = lNode.weight + rNode.weight;
parNode.leftNode = lNode;
parNode.rightNode = rNode;
//父节点必须往链表头添加 - 否则遇到weigth相同时,组件二叉树会混乱
list.addFirst(parNode);
Collections.sort(list);
System.out.println("遍历" + list);
//如果链表中只有一个元素,说明这个节点就是根节点
if(list.size() == 1) {
root = list.get(0);
flag = true;
break;
}
}
return flag;
}
private class Node<T> implements Comparable<Node> {
T data;
Integer weight;
Node<T> leftNode;
Node<T> rightNode;
public void preOrder(Node node, StringBuilder sb) {
sb.append(node.toString() + ", ");
if(node.leftNode != null) {
preOrder(node.leftNode, sb);
}
if(node.rightNode != null) {
preOrder(node.rightNode, sb);
}
}
public void inOrder(Node node, StringBuilder sb) {
if(node.leftNode != null) {
inOrder(node.leftNode, sb);
}
sb.append(node.toString() + ", ");
if(node.rightNode != null) {
inOrder(node.rightNode, sb);
}
}
public void setData(T data) {
this.data = data;
//节点的权重硬性规定为数据data内部的权重
try {
Field field = data.getClass().getDeclaredField("weight");
field.setAccessible(true);
weight = (Integer) field.get(data);
} catch (Exception e) {
e.printStackTrace();
}
}
@Override
public String toString() {
return "Node{" +
"data=" + data +
", weight=" + weight +
'}';
}
// node排序必须要实现这个函数 大于实参则大于0 小于则小于0 等于则等于0
@Override
public int compareTo(Node node) {
return this.weight - node.weight;
}
}
public static void main(String[] args) {
//1. 数据准备 - 为什么写那么麻烦,主要是写熟悉一些数组、链表之间的转换函数
Student student1 = new Student(1, "lrc", 8);
Student student2 = new Student(2, "qcj", 2);
Student student3 = new Student(3, "ert", 10);
Student student4 = new Student(4, "bfg", 5);
Student student5 = new Student(5, "ytu", 25);
Student[] stu = {
student1,student2,student3,student4,student5};
// 2 5 8 10 25
// 7 8 10 25
// 10 15 25
// 25 25
// 50
//2. 构造最优二叉树
OptimalBinaryTree<Student> tree = new OptimalBinaryTree(stu);
//3. 前序遍历二叉树
System.out.println(tree);
}
}
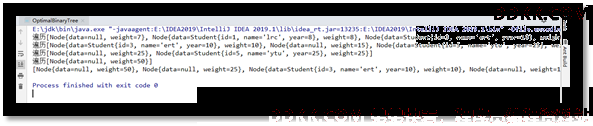
6. 平衡二叉树(AVL树)
1. AVL:是个发明者名字Adelson-Velsky-Landis Tree
2. 每个节点的左右子树的高度差不能大于1
Student.java
/**
* @Classname Student
* @Description
* @Date 2022/4/11 19:21
* @Created by lrc
*/
public class Student implements Comparable<Student> {
Integer id;
String name;
Integer year;
Integer weight;
public Student() {
}
public Student(Integer id, String name, Integer year) {
this.id = id;
this.name = name;
this.year = year;
this.weight = year;
}
public Integer getId() {
return id;
}
public void setId(Integer id) {
this.id = id;
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
public Integer getYear() {
return year;
}
public void setYear(Integer year) {
this.year = year;
this.weight = year;
}
@Override
public String toString() {
return "Student{" +
"id=" + id +
", name='" + name + '\'' +
", year=" + year +
'}';
}
@Override
public int compareTo(Student stu) {
Integer curId = this.getId();
Integer comapareId = stu.getId();
if(curId > comapareId) {
return 1;
}else if (curId < comapareId) {
return -1;
}else {
return 0;
}
}
}
注意:测试千万别用相同ID号的Student类 - 相同节点实在是太难处理
BalancedBinaryTree.java
/**
* @Classname BalancedBinaryTree
* @Description
* @Date 2022/4/15 11:05
* @Created by lrc
*/
public class BalancedBinaryTree<T> {
Node<T> root = null;
BalancedBinaryTree() {
}
BalancedBinaryTree(List<T> datas) {
for (T data : datas) {
add(data);
}
}
public static void main(String[] args) {
//数据准备
Student student1 = new Student(1, "lrc", 8);
Student student2 = new Student(2, "qcj", 2);
Student student3 = new Student(3, "ert", 10);
Student student33 = new Student(3, "rwerwe", 14);
Student student4 = new Student(4, "bfg", 5);
Student student5 = new Student(5, "ytu", 25);
Student student0 = new Student(0, "ytu", 25);
Student[] stu = {
student3, student2, student1, student4, student5, student33, student0};
List<Student> stuList = new ArrayList<>(Arrays.asList(stu));
//构造二叉树排序树
BalancedBinaryTree tree = new BalancedBinaryTree(stuList);
//前序遍历查看元素
/* System.out.println(tree.preOrder());
System.out.println("==================\n");*/
//删除元素 - 被删节点无左右子树
//tree.remove(student1);
//删除元素 - 被删节点有左右子树
//tree.remove(student3);
//删除元素 - 被删节点无左右子树
/* tree.remove(student2);
//前序遍历查看元素
System.out.println(tree.preOrder());
System.out.println("==================\n");*/
}
public void rightRotate() {
root.rightRotate();
}
//前序遍历元素
public String preOrder() {
StringBuilder sb = new StringBuilder();
root.preOrder(root, sb);
return sb.toString();
}
//添加元素
public void add(T data) {
if (root == null) {
root = new Node<T>();
root.data = data;
} else {
root.add(data, root, null);
}
System.out.println(preOrder());
System.out.println("===============\n");
}
//删除元素
public boolean remove(T data) {
boolean flag = root.remove(data);
return flag;
}
protected class Node<T> {
T data;
Node<T> leftNode;
Node<T> rightNode;
//返回当前节点右子树的高度
public int leftHeihgt() {
if (leftNode == null) {
return 0;
}
return leftNode.height();
}
//返回当前节点左子树的高度
public int rightHeight() {
if (rightNode == null) {
return 0;
}
return rightNode.height();
}
//计算当前节点的树高
public int height() {
return Math.max((leftNode == null ? 0 : leftNode.height()) + 1, (rightNode == null ? 0 : rightNode.height()) + 1);
}
//当前节点左旋
public boolean leftRotate() {
//1. 生成新节点跟当前节点差不多一样的信息 - 更改一下右节点信息即可
Node<T> newNode = new Node<>();
newNode.data = this.data;
newNode.leftNode = this.leftNode;
newNode.rightNode = this.rightNode.leftNode;
//2. 将根节点的信息由有右节点的信息取代,不过左节点是上面的新节点信息
this.data = rightNode.data;
this.rightNode = rightNode.rightNode;
this.leftNode = newNode;
return true;
}
//当前节点左旋
public boolean rightRotate() {
// System.out.println("发生右旋" + data);
//1. 生成新节点跟当前节点差不多一样的信息 - 更改一下左节点信息即可
Node<T> newNode = new Node<>();
newNode.data = this.data;
newNode.rightNode = this.rightNode;
newNode.leftNode = this.leftNode.rightNode;
//2. 将根节点的信息由有右节点的信息取代,不过右节点是上面的新节点信息
this.data = leftNode.data;
this.leftNode = this.leftNode.leftNode;
this.rightNode = newNode;
return true;
}
public void add(T data, Node<T> node, Node<T> parentNode) {
//确定 data 与 node.data的关系
Integer flag = node.compareTo(data);
;
//如果 data 大于 nodeData
if (flag <= 0) {
if (node.rightNode == null) {
Node<T> dataNode = new Node<>();
dataNode.data = data;
node.rightNode = dataNode;
} else {
add(data, node.rightNode, node);
}
如果 data 小于等于 nodeData 左节点添加
} else {
if (node.leftNode == null) {
Node<T> dataNode = new Node<>();
dataNode.data = data;
node.leftNode = dataNode;
} else {
add(data, node.leftNode, node);
}
}
//右旋
if(this.leftHeihgt() - this.rightHeight() > 1) {
if(parentNode.leftHeihgt() - parentNode.rightHeight() == 2) {
if(node.rightHeight() - node.leftHeihgt() == 1) {
node.leftRotate();
}
parentNode.rightRotate();
}
if(parentNode.leftHeihgt() - parentNode.rightHeight() == -2) {
if(node.leftHeihgt() - node.rightHeight() == 1) {
node.rightRotate();
}
parentNode.leftRotate();
}
if(parentNode.leftHeihgt() - parentNode.rightHeight() == 1) {
/* if(node.rightHeight() - node.leftHeihgt() == 1) {
node.leftRotate();
}*/
this.rightRotate();
}
if(parentNode.leftHeihgt() - parentNode.rightHeight() == -1) {
if(node.leftHeihgt() - node.rightHeight() == 1) {
node.rightRotate();
}
parentNode.leftRotate();
this.rightRotate();
}
}
//左旋
if(this.rightHeight() - this.leftHeihgt() > 1) {
if(parentNode.leftHeihgt() - parentNode.rightHeight() == 2) {
if(node.rightHeight() - node.leftHeihgt() == 1) {
node.leftRotate();
}
parentNode.rightRotate();
}
if(parentNode.leftHeihgt() - parentNode.rightHeight() == -2) {
if(node.leftHeihgt() - node.rightHeight() == 1) {
node.rightRotate();
}
parentNode.leftRotate();
}
if(parentNode.leftHeihgt() - parentNode.rightHeight() == 1) {
/* if(node.rightHeight() - node.leftHeihgt() == 1) {
node.leftRotate();
}*/
if(node.rightHeight() - node.leftHeihgt() == 1) {
node.leftRotate();
}
parentNode.rightRotate();
this.leftRotate();
}
if(parentNode.leftHeihgt() - parentNode.rightHeight() == -1) {
if(node.leftHeihgt() - node.rightHeight() == 1) {
node.rightRotate();
}
this.leftRotate();
}
}
}
public boolean remove(T data) {
Node<T> curNode = this;
Node<T> curNodeParentNode = null;
boolean isDeleted = false;
while (true) {
Integer flag = curNode.compareTo(data);
//找不到被删除的元素
if (curNode == null) {
break;
}
找到被删除的元素
if (flag == 0) {
//确定被删除元素与其父元素之间的关系
Integer flag2 = 0;
if (curNodeParentNode != null) {
flag2 = curNodeParentNode.compareTo(curNode.data);
}
//被删除节点没有子节点
if (curNode.leftNode == null && curNode.rightNode == null) {
if (flag2 > 0) {
curNodeParentNode.leftNode = null;
} else {
curNodeParentNode.rightNode = null;
}
//被删除元素有左右子节点 - 被删除元素由其右子树替代
} else if (curNode.leftNode != null && curNode.rightNode != null) {
//1. 更换被删除元素的数据为右节点的数据
curNode.data = curNode.rightNode.data;
//2. 将被删除元素的右子树中进行挂载
Node<T> temp = curNode.rightNode.leftNode;
curNode.rightNode.leftNode = null;
Node<T> temp2 = curNode.leftNode;
while (true) {
if (temp2.rightNode == null) {
temp2.rightNode = temp;
break;
}
temp2 = temp2.rightNode;
}
//3. 完成删除
curNode.rightNode = curNode.rightNode.rightNode;
//被删除元素只有一个子节点
} else {
if (curNode.leftNode != null) {
curNode.data = curNode.leftNode.data;
curNode.rightNode = curNode.leftNode.rightNode;
curNode.leftNode = curNode.leftNode.leftNode;
} else {
curNode.data = curNode.rightNode.data;
curNode.leftNode = curNode.rightNode.leftNode;
curNode.rightNode = curNode.rightNode.rightNode;
}
}
isDeleted = true;
break;
//当前节点大于被删除的data
} else if (flag > 0) {
curNodeParentNode = curNode;
curNode = curNode.leftNode;
//当前节点小于被删除的data
} else {
curNodeParentNode = curNode;
curNode = curNode.rightNode;
}
}
return true;
}
//前序遍历:中左右
private void preOrder(Node<T> node, StringBuilder sb) {
sb.append(node + "\n");
if (node.leftNode != null) {
preOrder(node.leftNode, sb);
}
if (node.rightNode != null) {
preOrder(node.rightNode, sb);
}
}
@Override
public String toString() {
return "Node{" +
"data=" + data +
'}';
}
//比较当前节点的data与实参的data大小关系
public int compareTo(T data) {
//确定 data 与 node.data的关系
Integer flag = 0;
try {
Method compareTo = this.data.getClass().getDeclaredMethod("compareTo", this.data.getClass());
flag = (Integer) compareTo.invoke(this.data, data);
} catch (Exception e) {
throw new RuntimeException("元素比较时发生异常,请检查代码");
}
return flag;
}
}
}

7. 多路查找树 - 多叉树
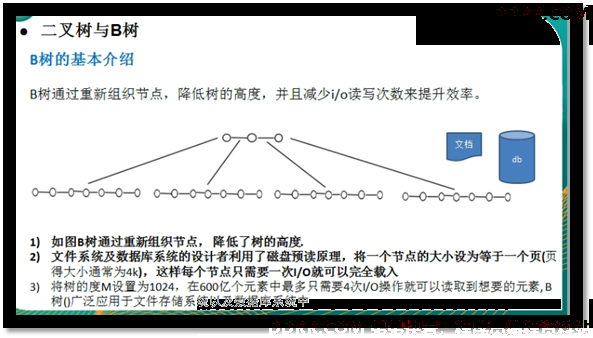
二叉树缺点
1、 二叉树需要加载到内存-数据很多,需要分多次访问硬盘读取这些数据进行组建二叉树;
2、 节点多,高度肯多高,高度高,节点遍历需要非常多次;
多路查找树分类
1、 B树、B-tree:每个节点都存储数据;
2-3树
2-3-4树
2、 B+树:只有叶子节点存储信息,叶子节点内元素有序、叶子节点间组成链表、非叶子节点只有导航的作用;
3、 B*树:B+树的变体,同级的节点使用链表连接;
7.1 B树 - 所有叶子节点必须在同一层
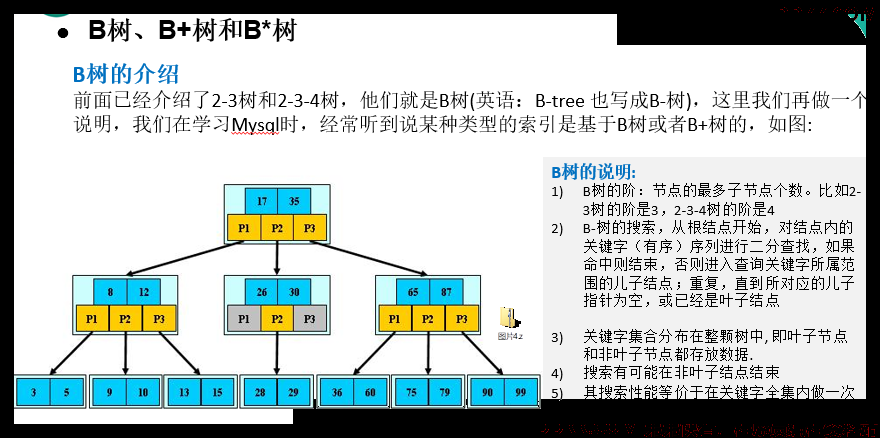
插入元素规则:2-3树为例