11、数据结构与算法 - 实战:查找算法
1. 顺序(线性)查找
思路:从头元素开始逐一开始与被查找元素比较 - 相等则返回,不想等则继续下一个元素,直至遍历完整个容器
public class SequentialSearch {
public static int search(int[] arrs, int value) {
for(int index = 0; index < arrs.length; index++) {
if(arrs[index] == value) {
return index;
}
}
return -1;
}
public static void main(String[] args) {
int[] arrs = {
1,-5,20,30,60};
int value = -20;
int index = search(arrs, value);
if(index != -1) {
System.out.println("查找到数值" + value + "在数组中的下标是" + index);
}else {
System.out.println("没有查找到");
}
}
}
2. 二分(折半)查找 - 有序的元素组
nlog 2
思路
- 先找中间元素下标 - midIndex = (left+right)/2
- 比较查找的元素searchValue与中间元素sortedArr[midIndex]
2.1 如果 searchValue > sortedArr[midIndex] - 向右半部分递归查找
2.2 如果 searchValue < sortedArr[midIndex] - 向左半部分递归查找
2.3 如果 searchValue = sortedArr[midIndex] - 返回midIndex
递归结束条件 - 满足任意一个即可
1、 left>right;
2、 searchValue=sortedArr[midIndex];
2.1 递归
public class BinarySearch {
//快速排序 - 递归
public static void quickSort(int[] array, int startIndex, int endIndex) {
if (startIndex >= endIndex)
return;
int left = startIndex;
int right = endIndex;
int temp = array[startIndex];
while (left < right) {
while (left < right && array[right] >= temp) right--;
array[left] = array[right];
array[right] = temp;
while (left < right && array[left] <= temp) left++;
array[right] = array[left];
array[left] = temp;
}
quickSort(array, startIndex, left - 1);
quickSort(array, left + 1, endIndex);
}
public static int[] sort(int[] arrs) {
int[] copyArr = arrs.clone();
quickSort(copyArr, 0, arrs.length - 1);
return copyArr;
}
//二分查找
public static int search(int[] arrs, int left, int right, int searchValue) {
//找不到直接返回-1
if (left > right) {
return -1;
} else {
int midIndex = (left + right) / 2;
if (searchValue > arrs[midIndex]) {
return search(arrs, midIndex + 1, right, searchValue);
} else if (searchValue < arrs[midIndex]) {
return search(arrs, left, midIndex - 1, searchValue);
} else {
return midIndex;
}
}
}
//查询查找元素的所有索引
public static Integer[] searchAllIndex(int[] arrs, int searchValue) {
int index = search(arrs, 0, arrs.length - 1, searchValue);
List<Integer> indexs = new ArrayList<>(arrs.length);
indexs.add(index);
if(index != -1) {
int currentIndex = index;
//往左寻找
while (true) {
currentIndex = currentIndex - 1;
if (currentIndex < 0)
break;
if (arrs[currentIndex] == searchValue) {
indexs.add(currentIndex);
} else {
break;
}
}
//往右寻找
currentIndex = index;
while (true) {
currentIndex = currentIndex + 1;
if (currentIndex == arrs.length)
break;
if (arrs[currentIndex] == searchValue) {
indexs.add(currentIndex);
} else {
break;
}
}
}
Integer[] indexss = new Integer[indexs.size()];
return indexs.toArray(indexss);
}
public static void main(String[] args) {
int[] a = {
4, 5, 10, 3, 1, 5, 7, 9};
int searchValue = 9;
int[] sortedArrs = sort(a);
int index = search(sortedArrs, 0, sortedArrs.length - 1, searchValue);
System.out.printf("未排序数组:%s\n", Arrays.toString(a));
System.out.printf("排序后数组:%s\n", Arrays.toString(sortedArrs));
if (index != -1) {
System.out.printf("查找的元素%d在排序数组中第%d位置\n", searchValue, index);
} else {
System.out.println("查找不到");
}
System.out.printf("查找的元素5在排序数组中所有位置是%s\n",Arrays.toString(searchAllIndex(sortedArrs,5)));
}
}
2.2 非递归 - 循环
//二分查找 - 非递归
public static int search(int[] arrs, int searchValue) {
int left = 0;
int right = arrs.length;
while(true) {
if (left > right) {
return -1;
}else {
Integer mid = (left + right)/2;
if(arrs[mid] == searchValue) {
return mid;
}
if(arrs[mid] > searchValue) {
right = mid - 1;
}else {
left = mid + 1;
}
}
}
}
3. 插值查找 - 有序的元素组
思路:跟二分查找差不多,只是中间索引公式不一样而已
中间索引有searchValue参与,自适应
使用场景
有序数组元素间差值分布比较一样 - 类似线性方程值
元素间分布不均匀不一定比二分查找快
二分查找中间索引公式: ( left + right )/2 → left + 1/2( right - left )
//其实就是上面公式的变种
插值查找中间索引公式: left + ( searchValue - arr[left] )/( arr[right]-arr[left] ) * ( right-left )
public class InsertSearch {
public static Integer[] search(int[] arrs, int left, int right, int searchValue) {
List<Integer> indexs = new ArrayList<Integer>(arrs.length);
//特点注意后面两个判断条件一定要加,-
// 因为midIndex有searchValue进行参与计算,一旦searchValue非常大时,一定会超出索引
// 当然你也可以在计算midIndex后进行判断是否超出数组范围。超过则返回-1 - 一样的效果
if(left > right || searchValue > arrs[arrs.length-1] || searchValue < arrs[0]) {
indexs.add(-1);
}else {
int midIndex = left + ( searchValue - arrs[left] )/( arrs[right]-arrs[left] ) * ( right-left );
if(searchValue > arrs[midIndex]) {
return search(arrs,midIndex+1, right, searchValue);
}else if(searchValue < arrs[midIndex]) {
return search(arrs,left, midIndex+1, searchValue);
}else {
indexs.add(midIndex);
//往左扫描
int curIndex = midIndex;
while(true) {
curIndex = curIndex - 1;
if(curIndex < 0) {
break;
}else {
if(arrs[curIndex] == searchValue) {
indexs.add(curIndex);
continue;
}
break;
}
}
//往右扫描
curIndex = midIndex;
while(true) {
curIndex = curIndex + 1;
if(curIndex == arrs.length) {
break;
}else {
if(arrs[curIndex] == searchValue) {
indexs.add(curIndex);
continue;
}
break;
}
}
}
}
Integer[] indexss = new Integer[indexs.size()];
return indexs.toArray(indexss);
}
public static void main(String[] args) {
int[] arrs = {
1,1,2,3,3,3,3,3,3,4,5,6,7};
String str = Arrays.toString(search(arrs,0, arrs.length-1, 3));
System.out.println(str);
}
}
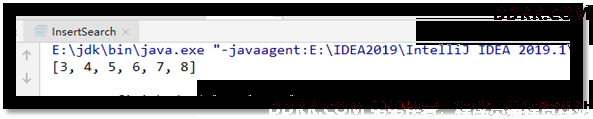
4. 斐波那契(黄金分隔)查找 - 有序的元素组
思路:跟二分查找类似 - 重要:将分割的两部分之间的长度比是黄金分割比即可 - 而Fibonacci数组相临两元素又无限接近黄金分割比 - 故将Fibonacci与黄金分割结合使用
# 二分查找midIndex
midIndex = (left+right)/2
# 黄金分隔查找midIndex
# 斐波那契数组相邻元素之间的比无限接近 黄金分割比0.618
# 重要:将分割的两部分之间的长度比是黄金分割比即可
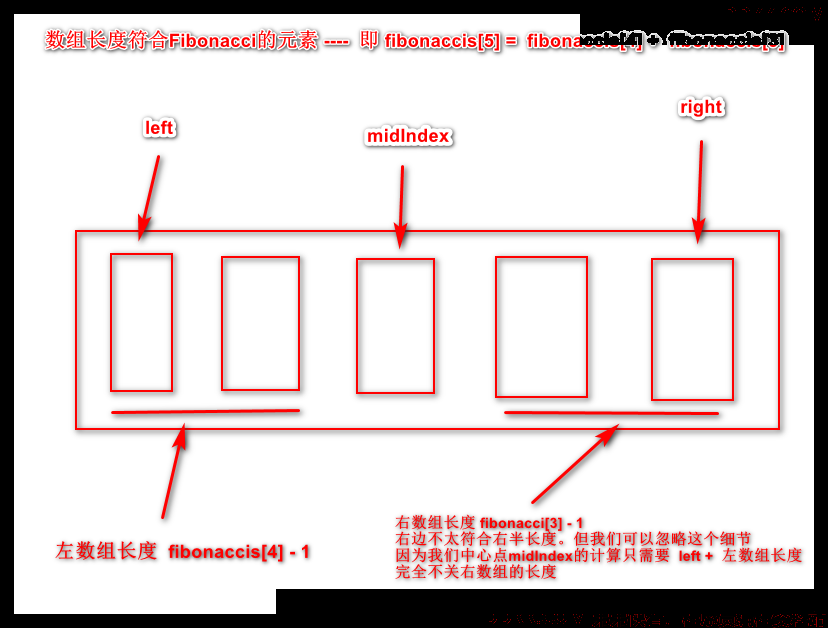
fibo(k) = fibo(k-1) + fibo(k-2)
# 二分法的思想就是找中心点进行比较 - 因为中心点占了一个位置故 左右总长度 fibo(k) -1
fibo(k) - 1 = ( fibo(k-1)-1 ) + ( fibo(k-2)-1 ) + 1
# 左边部分元素长度 = ( fibo(k-1)-1 )
# 右边部分元素长度 = ( fibo(k-2)-1 )
# 中心元素占一个位置 1
package top.linruchang.algorithm.search;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
/**
* @Classname FibonacciSearch
* @Description
* @Date 2022/4/11 13:32
* @Created by lrc
*/
public class FibonacciSearch {
// 返回斐波那契数列第index个位置的数字
public static int fiboNum(int index) {
if (index == 1 || index == 2) {
return 1;
} else {
return fiboNum(index - 1) + fiboNum(index - 2);
}
}
/**
* @param maxValue 斐波那契数列最后一个元素 大于 等于该元素
* @return
*/
public static Integer[] fibonacci3(int maxValue) {
List<Integer> fiboList = new ArrayList<>();
int length = 1;
while (true) {
int fiboNum = fiboNum(length);
fiboList.add(fiboNum);
if (fiboNum >= maxValue)
break;
length++;
}
Integer[] fiboNums = new Integer[fiboList.size()];
return fiboList.toArray(fiboNums);
}
/**
*
* @param arrs
* @param searchValue
* @return 如果最后返回null,说明没找到寻找元素的索引
*/
public static Integer[] search(Integer[] arrs, int searchValue) {
//存储找到的索引
List<Integer> indexs = new ArrayList<Integer>(arrs.length);
int left = 0;
int right ;
int midIndex;
int k; //斐波那契的索引
// 每个元素代表元素长度 -- fibonacci3最后一个元素代表 copyArr数组必须符合的数组长度。 -
Integer[] fibonacci3 = fibonacci3(arrs.length);
// 查看fibonacci3全部元素
System.out.printf("fibonacci数组:%s\n",Arrays.toString(fibonacci3));
// fibonacci3[K] 代表当前部分的长度
k = fibonacci3.length-1;
right = fibonacci3[k];
//构成成fibonacci3[K]长的数组 - 不符合则直接用arrs最后一个元素进行填充
Integer[] copyArr = Arrays.copyOf(arrs, fibonacci3[k]);
int index = arrs.length;
while (true) {
if (copyArr.length == index)
break;
copyArr[index] = arrs[arrs.length-1];
index++;
}
System.out.println("拷贝的数组:" + Arrays.toString(copyArr));
//数组索引小于0直接退出循环,说明找不到了
while(k != 0) {
midIndex = left + fibonacci3[k-1];
//准备右部分开始比较
if(copyArr[midIndex] < searchValue) {
left = midIndex + 1;
k-=2;
//准备左部分开始比较
}else if(copyArr[midIndex] > searchValue) {
right = midIndex - 1;
k--;
}else {
if(midIndex >= arrs.length-1) {
midIndex = arrs.length-1;
}
indexs.add(midIndex);
int currentIndex = midIndex;
//往左寻找
while (true) {
currentIndex = currentIndex - 1;
if (currentIndex < 0)
break;
if (arrs[currentIndex] == searchValue) {
indexs.add(currentIndex);
} else {
break;
}
}
//往右寻找
currentIndex = midIndex;
while (true) {
currentIndex = currentIndex + 1;
if (currentIndex == arrs.length)
break;
if (arrs[currentIndex] == searchValue) {
indexs.add(currentIndex);
} else {
break;
}
}
break;
}
}
if(indexs.size() == 0) {
return null;
}
Integer[] indexss = new Integer[indexs.size()];
return indexs.toArray(indexss);
}
public static void main(String[] args) {
Integer[] a = {
4, 5, 10, 15, 24, 36,36};
System.out.printf("原数组:%s\n" , Arrays.toString(a));
System.out.printf("寻找到的元素索引:%s",Arrays.toString(search(a, 36)));
}
}