15、算法与数据结构 - 实战:动态规划
什么是动态规划
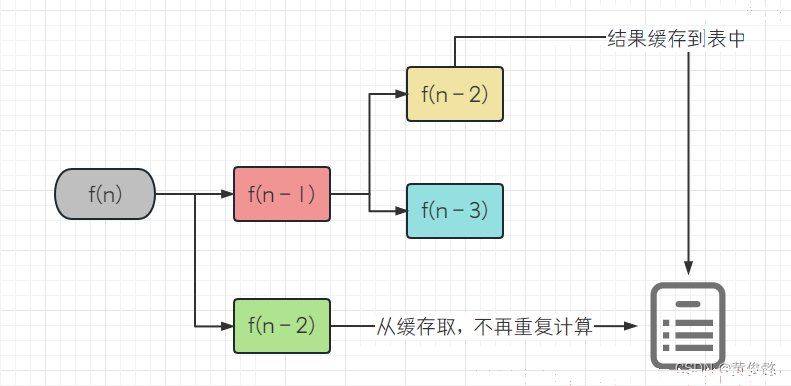
已经走过的分支,用一张表记着,下次遇到相同的分支,直接从表中拿值,不走重复的支路。
比如斐波那契数列,求f(n),则要计算f(n-1),f(n-2),而计算f(n-1)时,则要计算f(n-2),f(n-3),当计算完f(n-1),回到f(n)的计算,去计算f(n-2),其实前面已经算过,如果用一张表记着,所以这里就不用重复算。
1、假设有排成一行的N个位置,记为1~N,N 一定大于或等于 2,开始时机器人在其中的M位置上(M 一定是 1~N 中的一个)。如果机器人来到1位置,那么下一步只能往右来到2位置;如果机器人来到N位置,那么下一步只能往左来到 N-1 位置;如果机器人来到中间位置,那么下一步可以往左走或者往右走;规定机器人必须走 K 步,最终能来到P位置(P也是1~N中的一个)的方法有多少种?
/**
* 假设有排成一行的N个位置,记为1~N,N 一定大于或等于 2,
* 开始时机器人在其中的M位置上(M 一定是 1~N 中的一个)。
* 如果机器人来到1位置,那么下一步只能往右来到2位置;
* 如果机器人来到N位置,那么下一步只能往左来到 N-1 位置;
* 如果机器人来到中间位置,那么下一步可以往左走或者往右走;
* 规定机器人必须走 K 步,最终能来到P位置(P也是1~N中的一个)的方法有多少种?
* 给定四个参数 N、M、K、P,返回方法数。
* Created by huangjunyi on 2022/9/3.
*/
public class DynamicProgramming01 {
/**
* 暴力递归求解
* @param n 总位置数
* @param m 初始化位置
* @param k 可走步数
* @param p 目标位置
* @return
*/
public static int method01(int n, int m, int k, int p) {
// 不合法参数判断
if (n < 2 || k < 1 || m < 1 || m > n || p < 1 || p > n) return 0;
return processo1(n, m, k, p);
}
/**
* 暴力递归求解
* @param n 总位置数
* @param curr 当前位置
* @param remain 剩余可走步数
* @param p 目标位置
* @return
*/
private static int processo1(int n, int curr, int remain, int p) {
// base case:还剩0步要走,如果当前位置curr在目标位置p,则发现一种方法
if (remain == 0) return curr == p ? 1 : 0;
// 1位置,只能往右走
if (curr == 1) return processo1(n, 2, remain - 1, p);
// n位置,只能往左走
if (curr == n) return processo1(n, n - 1, remain - 1, p);
// 两个递归 往左走,往右走 返回的方法数累加
return processo1(n, n - 1, remain - 1, p) + processo1(n, n + 1, remain - 1, p);
}
/**
* 粗糙的动态规划,记忆化搜索
* @param n 总位置数
* @param m 初始化位置
* @param k 可走步数
* @param p 目标位置
* @return
*/
public static int method02(int n, int m, int k, int p) {
// 不合法参数判断
if (n < 2 || k < 1 || m < 1 || m > n || p < 1 || p > n) return 0;
// 初始化缓存表
int[][] dp = new int[n + 1][k + 1];
for (int i = 0; i <= n; i++) {
for (int j = 0; j <= k; k++) {
dp[i][j] = -1;
}
}
return processo2(n, m, k, p, dp);
}
/**
* 粗糙的动态规划,记忆化搜索
* @param n 总位置数
* @param curr 当前位置
* @param remain 剩余可走步数
* @param p 目标位置
* @param dp 记忆表
* @return
*/
private static int processo2(int n, int curr, int remain, int p, int[][] dp) {
// 如果缓存中有值,直接拿值,返回
if (dp[curr][remain] != -1) return dp[curr][remain];
if (remain == 0) {
dp[curr][remain] = curr == p ? 1 : 0;
return dp[curr][remain];
}
if (curr == 1) {
// 返回得到的值前,先存缓存表
dp[curr][remain] = processo2(n, 2, remain - 1, p, dp);
return dp[curr][remain];
}
if (curr == n) {
// 返回得到的值前,先存缓存表
dp[curr][remain] = processo2(n, n - 1, remain - 1, p, dp);
return dp[curr][remain];
}
// 返回得到的值前,先存缓存表
dp[curr][remain] = processo2(n, curr - 1, remain - 1, p, dp) + processo2(n, curr + 1, remain - 1, p, dp);
return dp[curr][remain];
}
/**
* 动态规划求解
* @param n 总位置数
* @param m 初始化位置
* @param k 可走步数
* @param p 目标位置
* @return
*/
public static int method03(int n, int m, int k, int p) {
// 不合法参数判断
if (n < 2 || k < 1 || m < 1 || m > n || p < 1 || p > n) return 0;
/*
dp表
dp[i][j]
表示当前在i位置
表示还剩j步要走
*/
int[][] dp = new int[n + 1][k + 1];
/*for (int i = 0; i <= n; i++) {
dp[i][0] = 0;
}
for (int j = 0; j <= k; k++) {
dp[0][j] = 0;
}*/
// 根据暴力递归的base case,初始化
dp[p][0] = 1;
/*
根据暴力递归的依赖关系,填表
dp[1][j]依赖dp[2][j-1]
dp[n][j]依赖dp[n-1][j-1]
dp[i][j]依赖dp[i-1][j-1]和dp[i+1][j-1]
*/
for (int remain = 1; remain <= k; remain++) {
for (int curr = 1; curr <= n; curr++) {
if (curr == 1) {
dp[curr][remain] = dp[2][remain - 1];
} else if (curr == n) {
dp[curr][remain] = dp[n - 1][remain - 1];
} else {
dp[curr][remain] = dp[curr + 1][remain - 1] + dp[curr - 1][remain - 1];
}
}
}
return dp[m][k];
}
}
2、背包问题(动态规划求解)
/**
* 背包问题(动态规划求解)
* Created by huangjunyi on 2022/9/3.
*/
public class DynamicProgramming02 {
public static int processByRecursive(int[] weights, int[] values, int bag) {
return byRecursive(weights, values, 0, bag);
}
/**
* 暴力递归
* @param weights 物品总量
* @param values 物品价值
* @param index 当前物品下标
* @param space 背包剩余空间
* @return
*/
private static int byRecursive(int[] weights, int[] values, int index, int space) {
if (space < 0 || index == weights.length) return 0;
// 当前位置物品不要,直接下一轮递归
int p1 = byRecursive(weights, values, index + 1, space);
int p2 = Integer.MIN_VALUE;
if (space >= weights[index]) {
//如果背包还有空间放得下当前物品,参数装入当前物品,进行下一轮递归
p2 = values[index] + byRecursive(weights, values, index + 1, space - weights[index]);
}
//递归返回,总p1,p2中取最大值
return Math.max(p1, p2);
}
/**
* 动态规划
* @param weights 物品总量
* @param values 物品价值
* @param bag 背包能承载的重量
* @return
*/
public static int processByDynamicProgramming(int[] weights, int[] values, int bag) {
int[][] dp = new int[values.length + 1][bag + 1];
for (int index = values.length - 1; index >= 0; index--) {
for (int remain = 0; remain <= bag; remain--) {
// 当前位置物品不要,直接下一轮递归
int p1 = dp[index + 1][remain];
int p2 = Integer.MIN_VALUE;
if (remain >= weights[index]) {
//如果背包还有空间放得下当前物品,参数装入当前物品,进行下一轮递归
p2 = values[index] + dp[index + 1][remain - weights[index]];
}
dp[index][remain] = Math.max(p1, p2);
}
}
return dp[0][bag];
}
}
3、给定一个只由数字组成的字符串,1对应A,2对应B…,将字符串的数据转化为字母,如11,可以转化为AA,也可以转化为K,问:有多少种转化结果
/**
* 给定一个只由数字组成的字符串,1对应A,2对应B...
* 将字符串的数据转化为字母,如11,可以转化为AA,也可以转化为K
* 问:有多少种转化结果
*/
public class DynamicProgramming03 {
public static int getThransferCountByRecursive(String str) {
char[] chars = str.toCharArray();
return process(chars, 0);
}
/**
* 暴力递归
* @param chars 数字字符数组
* @param i 当前位置
* @return
*/
private static int process(char[] chars, int i) {
if (i == chars.length) return 1;
int res = 0;
// 如当前位置字符是0,代表之前做的决定有问题
if (chars[i] == '0') return res;
res += process(chars, i + 1);
//当前数字位1,则有两个分支:1.只把当前数字转换为字母,2.把当前数字和下一位合在一起转换为字母
if (chars[i] == '1') {
if (i + 1 < chars.length) {
res += process(chars, i + 2);
}
}
//当前数字位2,只有在下一位数字是0~6之间,才有两个分支
if (chars[i] == '2') {
if (i + 1 < chars.length && chars[i + 1] >='0' && chars[i + 1] <= '6') {
res += process(chars, i + 2);
}
}
//返回累加结果
return res;
}
/**
* 动态规划
* @param str
* @return
*/
private static int getThransferCountByDp(String str) {
char[] chars = str.toCharArray();
// 因为暴力递归只有一个变化参数,所以改成动态规划后就以一位dp表
int[] dp = new int[chars.length + 1];
dp[chars.length] = 1;
for (int i = chars.length - 1; i >= 0; i--) {
int res = 0;
// 如当前位置字符是0,代表之前做的决定有问题
if (chars[i] == '0') {
dp[i] = 0;
continue;
}
//当前数字位1,则有两个分支:1.只把当前数字转换为字母,2.把当前数字和下一位合在一起转换为字母
res += dp[i + 1];
if (chars[i] == '1') {
if (i + 1 < chars.length) {
res += dp[i + 2];
}
}
//当前数字位2,只有在下一位数字是0~6之间,才有两个分支
if (chars[i] == '2') {
if (i + 1 < chars.length && chars[i + 1] >='0' && chars[i + 1] <= '6') {
res += dp[i + 2];
}
}
dp[i] = res;
}
return dp[0];
}
public static void main(String[] args) {
System.out.println(getThransferCountByRecursive("11111"));
System.out.println(getThransferCountByDp("11111"));
}
}
4、给定一个整形数组,代表一串纸牌,有A、B两个玩家,从中抽取纸牌,但是每次只能拿最左或者最右,假设两个玩家绝顶聪明,求最后获胜方的结果值
比如有一串纸牌50、100、20、10
因为两个玩家都绝顶聪明
先手玩家如果拿了50,后手玩家就能拿100,那么他就输了,所以他不会拿50,他会先拿10
然后剩下50、100、20
然后后手玩家看,无论拿最左还是最右的牌,他都会输,所以他只能去拿较大的牌,
然后先手玩家拿走100
所以先手玩家是必赢的
因此返回获胜方是先手玩家
假设这一串纸牌非常长,返回最后获胜的是谁
/**
* 给定一个整形数组,代表一串纸牌
* 有A、B两个玩家,从中抽取纸牌,但是每次只能拿最左或者最右
* 假设两个玩家绝顶聪明(博弈)
* 求最后获胜方的结果值
* Created by huangjunyi on 2022/9/3.
*/
public class DynamicProgramming04 {
/**
* 先手拿牌
* @param values
* @param left
* @param right
* @return
*/
public static int first(int[] values, int left, int right) {
// 只剩下一张牌,先手拿走
if (left == right) return values[left];
// 因为先手决定聪明,会拿走最大的分数
return Math.max(
// 拿走最左侧牌,然后先手就转为后手了,调后手函数,获得剩下的分数
values[left] + second(values, left + 1, right),
// 拿走最右侧牌,然后先手就转为后手了,调后手函数,获得剩下的分数
values[right] + second(values, left, right - 1)
);
}
/**
* 后手拿牌
* @param values
* @param left
* @param right
* @return
*/
public static int second(int[] values, int left, int right) {
// 只剩下一张牌,会被先手拿走,后手拿不到
if (left == right) return 0;
// 因为先手决定聪明,会让后手拿到最小的分数
return Math.min(
// 最左侧牌被先手拿走,后手转为先手,在left+1~right上调先手函数做决定
first(values, left + 1, right),
// 最右侧牌被先手拿走,后手转为先手,在left~right-1上调先手函数做决定
first(values, left, right - 1)
);
}
/**
* 暴力递归
* @param values
* @return
*/
public static int getWinValue(int[] values) {
return Math.max(
// 先手玩家获得的分数
first(values, 0, values.length - 1),
// 后手玩家获得的分数
second(values, 0, values.length - 1)
);
}
/**
* 先手拿牌
* @param values
* @param left
* @param right
* @param firstMap
*@param secondMap @return
*/
public static int firstByCacheMap(int[] values, int left, int right, int[][] firstMap, int[][] secondMap) {
// 如果缓存中有值,直接返回缓存中的值
if (firstMap[left][right] != -1) return firstMap[left][right];
int res = 0;
// 只剩下一张牌,先手拿走
if (left == right) res = values[left];
// 因为先手决定聪明,会拿走最大的分数
else res = Math.max(
// 拿走最左侧牌,然后先手就转为后手了,调后手函数,获得剩下的分数
values[left] + secondByCacheMap(values, left + 1, right, firstMap, secondMap),
// 拿走最右侧牌,然后先手就转为后手了,调后手函数,获得剩下的分数
values[right] + secondByCacheMap(values, left, right - 1, firstMap, secondMap)
);
// 记录缓存表
firstMap[left][right] = res;
return res;
}
/**
* 后手拿牌
* @param values
* @param left
* @param right
* @param firstMap
*@param secondMap @return
*/
public static int secondByCacheMap(int[] values, int left, int right, int[][] firstMap, int[][] secondMap) {
// 如果缓存中有值,直接返回缓存中的值
if (secondMap[left][right] != -1) return secondMap[left][right];
int res = 0;
// 只剩下一张牌,会被先手拿走,后手拿不到
if (left == right) res = 0;
// 因为先手决定聪明,会让后手拿到最小的分数
else res = Math.min(
// 最左侧牌被先手拿走,后手转为先手,在left+1~right上调先手函数做决定
firstByCacheMap(values, left + 1, right, firstMap, secondMap),
// 最右侧牌被先手拿走,后手转为先手,在left~right-1上调先手函数做决定
firstByCacheMap(values, left, right - 1, firstMap, secondMap)
);
// 记录缓存表
secondMap[left][right] = res;
return res;
}
/**
* 暴力递归改成记忆化搜索
* @param values
* @return
*/
public static int getWinValueByCacheMap(int[] values) {
// 因为暴力递归中,有两个函数,先后,后手,所以搞两个缓存表
int[][] firstMap = new int[values.length][values.length];
int[][] secondMap = new int[values.length][values.length];
// 初始化缓存表
for (int i = 0; i < values.length; i++) {
for (int j = 0; j < values.length; j++) {
firstMap[i][j] = -1;
secondMap[i][j] = -1;
}
}
return Math.max(
// 先手玩家获得的分数
firstByCacheMap(values, 0, values.length - 1, firstMap, secondMap),
// 后手玩家获得的分数
secondByCacheMap(values, 0, values.length - 1, firstMap, secondMap)
);
}
/**
* 动态规划
* @param values
* @return
*/
public static int getWinValueByDp(int[] values) {
int n = values.length;
// 因为暴力递归中,有两个函数,先后,后手,所以搞两个dp表
int[][] first = new int[n][n];
int[][] second = new int[n][n];
// 根据暴力递归先手函数的base case(if (left == right) return values[left];),初始化first
for (int i = 0; i < n; i++) {
first[i][i] = values[i];
}
/*
根据暴力递归推断dp表的依赖关系
first[i][j]依赖second[i+1][j]和second[i][j-1]
second[i][j]依赖first[i+1][j]和first[i][j-1]
所以依着对角线从上往下填,从左往右填完所有对角线就ok
因为left <= right,所以,左下半部分不需要填
因为0对角线已经初始化了,从1对角线开始
*/
for (int i = 1; i < n; i++) {
int left = 0; // 行
int right = i; // 列
while (left < n - 1 && right < n) {
first[left][right] = Math.max(values[left] + second[left + 1][right], values[right] + second[left][right - 1]);
second[left][right] = Math.min(first[left + 1][right], first[left][right - 1]);
// 依着对角线填,所以行++,列++
left++;
right++;
}
}
return Math.max(first[0][n - 1], second[0][n - 1]);
}
public static void main(String[] args) {
int[] values = {
1,2,5,23,8,3,122,8};
System.out.println(getWinValue(values));
System.out.println(getWinValueByCacheMap(values));
System.out.println(getWinValueByDp(values));
}
}
5、货币组合问题
- 给定一个整形数组arr表示一组不同面值的货币
- 给定一个整形aim,表示需要通过不同的货币拼凑一起到总额aim
- 从arr中取货币,每种货币都可以取若干张
- 求有多少种组合方法
/**
* 货币组合问题
* 给定一个整形数组arr表示一组不同面值的货币
* 给定一个整形aim,表示需要通过不同的货币拼凑一起到总额aim
* 从arr中取货币,每种货币都可以取若干张
* 求有多少种组合方法
* Created by huangjunyi on 2022/9/3.
*/
public class DynamicProgramming05 {
public static int method01(int[] arr, int aim) {
if (arr == null || arr.length == 0 || aim < 0) return 0;
return process01(arr, 0, aim);
}
/**
* 暴力递归
* @param arr 货币数组
* @param index 当前货币
* @param remain 剩余要组出的总额
* @return
*/
private static int process01(int[] arr, int index, int remain) {
if (index == arr.length) return remain == 0 ? 1 : 0;
int res = 0;
// index位置的货币,用0张、用1张、用2张......
for (int i = 0; i * arr[index] <= remain; i++)
res += process01(arr, index + 1, remain - i * arr[index]);
return res;
}
public static int method02(int[] arr, int aim) {
if (arr == null || arr.length == 0 || aim < 0) return 0;
// 定义并初始化缓存表
int[][] dp = new int[arr.length + 1][aim + 1];
for (int i = 0; i <= arr.length; i++) for (int j = 0; j <= aim; j++) dp[i][j] = -1;
return process02(arr, 0, aim, dp);
}
/**
* 记忆化搜索
* @param arr 货币数组
* @param index 当前货币
* @param remain 剩余要组出的总额
* @return
*/
private static int process02(int[] arr, int index, int remain, int[][] dp) {
// 命中缓存,返回
if (dp[index][remain] != -1) return dp[index][remain];
if (index == arr.length) return dp[index][remain] = remain == 0 ? 1 : 0;
int res = 0;
// index位置的货币,用0张、用1张、用2张......
for (int i = 0; i * arr[index] <= remain; i++)
res += process02(arr, index + 1, remain - i * arr[index], dp);
// 记录到缓存,然后返回
return dp[index][remain] = res;
}
/**
* 动态规划
* @param arr
* @param aim
* @return
*/
public static int method03(int[] arr, int aim) {
if (arr == null || arr.length == 0 || aim < 0) return 0;
/*
dp[index][remain]
index往后的货币任意选择,凑够remain元,有几种方法
观察暴力递归可知
dp[index][remain]依赖于index+1行的格子
*/
int[][] dp = new int[arr.length + 1][aim + 1];
// base case:if (index == arr.length) return remain == 0 ? 1 : 0;
dp[arr.length][0] = 1;
for (int index = arr.length - 1; index >= 0; index--)
for (int remain = 0; remain <= aim; remain++)
// index位置的货币,用0张、用1张、用2张......
for (int i = 0; i * arr[index] <= remain; i++)
dp[index][remain] += dp[index + 1][remain- i * arr[index]];
return dp[0][aim];
}
/**
* 动态规划,枚举优化
* @param arr
* @param aim
* @return
*/
public static int method04(int[] arr, int aim) {
if (arr == null || arr.length == 0 || aim < 0) return 0;
int[][] dp = new int[arr.length + 1][aim + 1];
dp[arr.length][0] = 1;
for (int index = arr.length - 1; index >= 0; index--)
for (int remain = 0; remain <= aim; remain++)
/*
观察:
dp[index][remain] = dp[index + 1][remain] + dp[index + 1][remain - 1 * arr[index]] - dp[index + 1][remain - 2 * arr[index]] - ......
dp[index][remain - 1 * arr[index]] = dp[index + 1][remain - 1 * arr[index]] - dp[index + 1][remain - 2 * arr[index]] - ......
所以:
dp[index][remain] = dp[index + 1][remain] + dp[index][remain - 1 * arr[index]]
因此省去了for循环的枚举行为
*/
dp[index][remain] = remain >= arr[index] ?
dp[index + 1][remain] + dp[index][remain - arr[index]] :
dp[index + 1][remain];
return dp[0][aim];
}
public static void main(String[] args) {
int[] arr = {
5, 10, 50, 100};
int aim = 1000;
System.out.println(method01(arr, aim));
System.out.println(method02(arr, aim));
System.out.println(method03(arr, aim));
System.out.println(method04(arr, aim));
}
}
6、给定一个字符串str,给定一个字符串类型的数组arr,出现的字符都是小写英文。arr每一个字符串,代表一张贴纸,你可以把单个字符剪开使用,目的是拼出str来。返回需要至少多少张贴纸可以完成这个任务。例子:str= “babac”,arr = {“ba”,“c”,“abcd”}。ba + ba + c 3张, abcd + abcd 2张, abcd + ba 2张。所以返回2。
这一题也是先写出暴力递归,就很好改成动态规划,但是只需改出记忆化搜索就可以了,因为它的暴力递归的可变参数,是一个字符串,无法确定范围
/**
* 给定一个字符串str,给定一个字符串类型的数组arr,出现的字符都是小写英文。
* arr每一个字符串,代表一张贴纸,你可以把单个字符剪开使用,目的是拼出str来。返回需要至少多少张贴纸可以完成这个任务。
* 例子:str= "babac",arr = {"ba","c","abcd"}。ba + ba + c 3张, abcd + abcd 2张, abcd + ba 2张。所以返回2。
* Created by huangjunyi on 2022/9/3.
*/
public class DynamicProgramming06 {
/**
* 暴力递归
* @param str 目标字符串
* @param arr 贴纸数组
* @return
*/
public static int getMin01(String str, String[] arr) {
int res = process01(str, arr);
return res == Integer.MAX_VALUE ? -1 : res;
}
/**
* 暴力递归
* @param str 剩余字符串
* @param arr 贴纸数组
* @return
*/
private static int process01(String str, String[] arr) {
// 字符串已经拼好,还需0张贴纸
if (str.length() == 0) return 0;
int min = Integer.MAX_VALUE;
// 尝试每一张贴纸
for (int i = 0; i < arr.length; i++) {
// 减去选择的贴纸的字符,返回新的剩余要拼的字符串
String newStr = getNewStr(str, arr[i]);
// 选择的贴纸没有削去任何一个字符,无效,跳过
if (newStr.length() == str.length()) continue;
// 剩余字符串newStr,往下继续跑递归
min = Math.min(min, process01(newStr, arr));
}
// 算上自己使用的一张贴纸
if (min != Integer.MAX_VALUE) min += 1;
return min;
}
/**
* 原字符串,减去贴纸中的字符,返回新的字符串
* @param s1 原字符串
* @param s2 贴纸
* @return
*/
private static String getNewStr(String s1, String s2) {
char[] chs1 = s1.toCharArray();
char[] chs2 = s2.toCharArray();
int[] count = new int[26];
// 统计原字符串的各种字符数
for (int i = 0; i < chs1.length; i++) {
count[chs1[i] - 'a']++;
}
// 减去贴纸含有的各种字符的字符数
for (int i = 0; i < chs2.length; i++) {
count[chs2[i] - 'a']--;
}
// 拼接处新的剩余字符串
StringBuilder sb = new StringBuilder();
for (int i = 0; i < count.length; i++) {
if (count[i] > 0) {
for (int j = 0; j < count[i]; j++) {
sb.append((char)(i + 'a'));
}
}
}
return sb.toString();
}
public static int getMin(String str, String[] arr) {
/*
map记录每种贴纸的字符出现的个数
例如map[i][0] 表示第i张贴纸,a字符出现的次数(a - a == 0)
初始化号map表
*/
int[][] map = new int[arr.length][26];
for (int i = 0; i < arr.length; i++) {
char[] chars = arr[i].toCharArray();
for (char aChar : chars) {
map[i][aChar - 'a'] += 1;
}
}
// 缓存表,key剩余字符串,value需要的贴纸数,一个一维表,因为暴力递归中只有一个可变参数(剩余字符串)
Map<String, Integer> dp = new HashMap<>();
dp.put("", 0);
return process(str, map, dp);
}
private static int process(String remain, int[][] map, Map<String, Integer> dp) {
// 如果缓存表有值,直接返回
if (dp.containsKey(remain)) return dp.get(remain);
// 统计原字符串的各种字符数
char[] chars = remain.toCharArray();
int[] temp = new int[26];
for (char aChar : chars) {
temp[aChar - 'a'] += 1;
}
int res = Integer.MAX_VALUE;
// 尝试每一张贴纸
for (int i = 0; i < map.length; i++) {
StringBuilder sb = new StringBuilder();
// 优化,只选择能消除掉当前字符串第一个字符的贴纸(因为第一个字符串总要消掉的,先消后消不会影响结果)
if (map[i][chars[0] - 'a'] == 0) continue;
// 减去贴纸含有的各种字符的字符数
for (int j = 0; j < 26; j++) {
for (int k = 0; k < Math.max(0, temp[j] - map[i][j]); k++) {
sb.append((char) (j + 'a'));
}
}
// 剩余字符串newStr,往下继续跑递归
int next = process(sb.toString(), map, dp);
// next + 1 算上自己使用的一张贴纸
if (next != -1) res = Math.min(res, next + 1);
}
// 结果返回前,先放入缓存表
dp.put(remain, res == Integer.MAX_VALUE ? -1 : res);
return dp.get(remain);
}
public static void main(String[] args) {
String str = "babac";
String[] arr = {
"ba","c","abcd"};
System.out.println(getMin01(str, arr));
System.out.println(getMin(str, arr));
}
}
7、求两个字符串的最长公共子序列长度
/**
* 求两个字符串的最长公共子序列长度
* Created by huangjunyi on 2022/9/3.
*/
public class DynamicProgramming07 {
/**
* 暴力递归
* @param str1
* @param str2
* @return
*/
public static int getMaxCommon01(String str1, String str2) {
char[] chars1 = str1.toCharArray();
char[] chars2 = str2.toCharArray();
return process01(chars1, chars2, chars1.length - 1, chars2.length - 1);
}
/**
* 求chars1从0到r1与chars2从0到r2的最长公共子序列长度
* @param chars1
* @param chars2
* @param r1
* @param r2
* @return
*/
private static int process01(char[] chars1, char[] chars2, int r1, int r2) {
if (r1 == 0 && r2 == 0) {
// 只剩一个字符,相等时1,不等是0
return chars1[r1] == chars2[r2] ? 1 : 0;
} else if (r1 == 0) {
// chars1只剩一个字符,如果和chars2[r2]相等,返回1,不等看chars2前面的字符
return chars1[r1] == chars2[r2] ? 1 : process01(chars1, chars2, r1, r2 - 1);
} else if (r2 == 0) {
// chars2只剩一个字符,如果和chars1[r1]相等,返回1,不等看chars1前面的字符
return chars1[r1] == chars2[r2] ? 1 : process01(chars1, chars2, r1 - 1, r2);
} else {
// 不要r1,看公共子序列多长
int p1 = process01(chars1, chars2, r1 - 1, r2);
// 不要r2,看公共子序列多长
int p2 = process01(chars1, chars2, r1, r2 - 1);
// r1 == r2,看公共子序列多长
int p3 = chars1[r1] == chars2[r2] ? process01(chars1, chars2, r1 - 1, r2 - 1) : 0;
// 三个结果PK
return Math.max(Math.max(p1, p2), p3);
}
}
/**
* 改成动态规划
* @param str1
* @param str2
* @return
*/
public static int getMaxCommon(String str1, String str2) {
char[] chars1 = str1.toCharArray();
char[] chars2 = str2.toCharArray();
/*
dp[r1][r2]:
chars1从0到r1与chars2从0到r2的最长公共子序列长度
*/
int[][] dp = new int[chars1.length][chars2.length];
// if (r1 == 0 && r2 == 0)
dp[0][0] = chars1[0] == chars2[0] ? 1 : 0;
// else if (r1 == 0)
for (int i = 1; i < chars2.length; i++) {
dp[0][i] = Math.max(dp[0][i-1], chars2[i] == chars1[0] ? 1 : 0);
}
// else if (r2 == 0)
for (int i = 1; i < chars1.length; i++) {
dp[i][0] = Math.max(dp[i-1][0], chars1[i] == chars2[0] ? 1 : 0);
}
// else
for (int i = 1; i < chars1.length; i++) {
for (int j = 1; j < chars2.length; j++) {
dp[i][j] = Math.max(dp[i-1][j], dp[i][j-1]);
if (chars1[i] == chars2[j]) dp[i][j] = Math.max(dp[i][j], dp[i-1][j-1] + 1);
}
}
return dp[chars1.length - 1][chars2.length - 1];
}
}
8、给定一个数组,代表每个人喝完咖啡准备刷杯子的时间,只有一台咖啡机,一次只能洗一个杯子,时间耗费a,洗完才能洗下一杯,每个咖啡杯也可以自己挥发干净,时间耗费b,咖啡杯可以并行挥发,返回让所有咖啡杯变干净的最早完成时间。三个参数: int[] arr、int a、 int b
/**
* 给定一个数组,代表每个人喝完咖啡准备刷杯子的时间
* 只有一台洗咖啡机,一次只能洗一个杯子,时间耗费a,洗完才能洗下一杯
* 每个咖啡杯也可以自己挥发干净,时间耗费b,咖啡杯可以并行挥发
* 返回让所有咖啡杯变干净的最早完成时间
* 三个参数: int[] arr、int a、 int b
* Created by huangjunyi on 2022/9/4.
*/
public class DynamicProgramming08 {
public static int processByRecursive(int[] arr, int a, int b) {
return processByRecursive(arr, a, b, 0, 0);
}
/**
* 暴力递归
* @param arr 每个人喝完咖啡准备刷杯子的时间
* @param a 洗杯子花费的时间
* @param b 杯子挥发干净的时间
* @param index 当前的杯子
* @param washLine 咖啡机可以使用的时间
* @return
*/
private static int processByRecursive(int[] arr, int a, int b, int index, int washLine) {
//已经到了最后一个杯子,手洗和挥发,选结束时间早的
//但是如果选手洗,要看喝完咖啡和洗咖啡机能用的时间,哪个比较晚
if (index == arr.length - 1) return Math.min(Math.max(arr[index], washLine) + a, arr[index] + b);
//当前杯子选择使用洗咖啡机,洗完的时间
int time1 = Math.max(arr[index], washLine) + a;
//其他杯子也都干净的时间,因为选择了使用洗咖啡机,所以洗咖啡机能用的时间要更新
int time2 = processByRecursive(arr, a, b, index + 1, time1);
//两个时间PK
int p1 = Math.max(time1, time2);
//当前杯子选择挥发,挥发干净的时间
int time3 = arr[index] + b;
//其他杯子也都干净的时间
int time4 = processByRecursive(arr, a, b, index + 1, washLine);
//两个时间PK
int p2 = Math.max(time3, time4);
//两个时间取最小
return Math.min(p1, p2);
}
/**
* 动态规划
* @param arr 每个人喝完咖啡准备刷杯子的时间
* @param a 洗杯子花费的时间
* @param b 杯子挥发干净的时间
* @return
*/
private static int processByDp(int[] arr, int a, int b) {
/*
应为暴力递归中是两个可变参数,所以改成动态规划是一张二维表
但是第二个参数washLine有点难估计,属于业务限制模型
所以就看所有杯子都选择用洗咖啡机洗,最大能冲到什么时间
*/
int washLineLimit = 0;
for (int i = 0; i < arr.length; i++) {
washLineLimit = Math.max(washLineLimit, arr[i]) + a;
}
// dp[i][j] 从i号杯子开始,洗咖啡机j时间点可以用,所有杯子干净需要的时间
int[][] dp = new int[arr.length][washLineLimit + 1];
// 根据base case初始化dp表
// 已经到了最后一个杯子,手洗和挥发,选结束时间早的
// 但是如果选手洗,要看喝完咖啡和洗咖啡机能用的时间,哪个比较晚
// if (index == arr.length - 1) return Math.min(Math.max(arr[index], washLine) + a, arr[index] + b);
for (int i = 0; i <= washLineLimit; i++) {
dp[arr.length - 1][i] = Math.min(Math.max(arr[arr.length - 1], i) + a, arr[arr.length - 1] + b);
}
for (int i = arr.length - 2; i >= 0; i--) {
for (int j = 0; j <= washLineLimit; j++) {
// 当前杯子选择用洗咖啡机洗,洗完的时间
int p1 = Integer.MAX_VALUE;
int time1 = Math.max(arr[i], j) + a;
// 判断越界,如果当前杯子选择用洗咖啡机洗,洗完时间超过washLineLimit,是无效情况,跳过
if (time1 > washLineLimit) continue;
//其他杯子也都干净的时间,因为选择了使用洗咖啡机,所以洗咖啡机能用的时间要更新
int time2 = dp[i + 1][time1];
//两个时间PK
p1 = Math.max(time1, time2);
//当前杯子选择挥发,挥发干净的时间
int time3 = arr[i] + b;
//其他杯子也都干净的时间
int time4 = dp[i + 1][j];
//两个时间PK
int p2 = Math.max(time3, time4);
//两个时间取最小
dp[i][j] = Math.min(p1, p2);
}
}
// return processByRecursive(arr, a, b, 0, 0);
return dp[0][0];
}
public static void main(String[] args) {
int[] arr = {
1,1,5,5,7,10,12,12,12,12,12,12,15};
int a=3;
int b=10;
System.out.println(processByRecursive(arr, a, b));
System.out.println(processByDp(arr, a, b));
}
}
9、马踏棋盘问题
- 规定马从0,0位置出发,棋盘是10*9大小的棋盘
- 给定三个整形变量x,y,k,表示马走k步到达x,y位置
- 问有几种走法
/**
* 马踏棋盘问题
* 规定马从0,0位置出发,棋盘是10*9大小的棋盘
* 给定三个整形变量x,y,k,表示马走k步到达x,y位置
* 问有几种走法
* Created by huangjunyi on 2022/9/4.
*/
public class DynamicProgramming09 {
public static int processByRecursive(int x, int y, int k) {
// 越界返回0
if (x < 0 || x >= 10 || y < 0 || y >= 9) return 0;
// 剩余0步要走,如果到达目标位置,返回1,代表一种走法,否则返回0
if (k == 0) return x == 0 && y == 0 ? 1 : 0;
// 从(x,y)位置,反方向走,往8个方向跳,累加跳回到起点的方法数,就等于从起点跳到(x,y)的方法数
return processByRecursive(x + 2, y + 1, k - 1) +
processByRecursive(x + 1, y + 2, k - 1) +
processByRecursive(x - 1, y + 2, k - 1) +
processByRecursive(x - 2, y + 1, k - 1) +
processByRecursive(x - 2, y - 1, k - 1) +
processByRecursive(x - 1, y - 2, k - 1) +
processByRecursive(x + 1, y - 2, k - 1) +
processByRecursive(x + 2, y - 1, k - 1);
}
public static int processByDp(int x, int y, int k) {
// 三个变化参数,所以准备一张3维表
int[][][] dp = new int[10][9][k + 1];
// base case:if (k == 0) return x == 0 && y == 0 ? 1 : 0;
dp[0][0][0] = 1;
/*
观察暴力递归
剩k步时的答案,依赖剩k-1步时的答案
所以上层答案依赖下一层,不依赖本层
已就是dp[i][j][k]依赖dp[x][y][k-1]
*/
for (int level = 1; level <= k; level++) {
for (int i = 0; i < 10; i++) {
for (int j = 0; j < 9; j++) {
dp[i][j][level] =
// 从(x,y)位置,反方向走,往8个方向跳,累加跳回到起点的方法数,就等于从起点跳到(x,y)的方法数
getFromDp(dp, i + 2, j + 1, level - 1) +
getFromDp(dp, i + 1, j + 2, level - 1) +
getFromDp(dp, i - 1, j + 2, level - 1) +
getFromDp(dp, i - 2, j + 1, level - 1) +
getFromDp(dp, i - 2, j - 1, level - 1) +
getFromDp(dp, i - 1, j - 2, level - 1) +
getFromDp(dp, i + 1, j - 2, level - 1) +
getFromDp(dp, i + 2, j - 1, level - 1);
}
}
}
return dp[x][y][k];
}
public static int getFromDp(int[][][] dp, int x, int y, int k) {
if (x < 0 || x >= 10 || y < 0 || y >= 9) return 0;
return dp[x][y][k];
}
public static void main(String[] args) {
System.out.println(processByRecursive(6, 8, 10));
System.out.println(processByDp(6, 8, 10));
}
}
10、最长回文子序列
力扣516题
https://leetcode.cn/problems/longest-palindromic-subsequence/description/
给你一个字符串 s ,找出其中最长的回文子序列,并返回该序列的长度。
子序列定义为:不改变剩余字符顺序的情况下,删除某些字符或者不删除任何字符形成的一个序列。
/**
* https://leetcode.cn/problems/longest-palindromic-subsequence/
* 给你一个字符串 s ,找出其中最长的回文子序列,并返回该序列的长度。
* 子序列定义为:不改变剩余字符顺序的情况下,删除某些字符或者不删除任何字符形成的一个序列。
* Created by huangjunyi on 2022/11/27.
*/
public class DynamicProgramming10 {
/**
* 动态规划
*/
class Solution {
public int longestPalindromeSubseq(String s) {
char[] chs = s.toCharArray();
int N = chs.length;
// l和r两个可变参数,l和r的变化返回都是0~N-1
int[][] dp = new int[N][N];
/*
初始化dp表的两种情况
剩一个字符
剩两个字符
if (l == r) return 1;
if (l == r - 1) return chs[l] == chs[r] ? 2 : 0;
*/
dp[N-1][N-1] = 1;
for (int i = 0; i < N - 1; i++) {
dp[i][i] = 1;
dp[i][i + 1] = chs[i] == chs[i + 1] ? 2 : 1;
}
for (int l = N - 2; l >= 0; l--) {
for (int r = l + 2; r < N; r++) {
// 不要l字符和r字符
int p1 = dp[l + 1][r - 1];
// 不要l字符
int p2 = dp[l + 1][r];
// 不要r字符
int p3 = dp[l][r - 1];
// l字符和r字符相等,要
int p4 = chs[l] == chs[r] ? 2 + dp[l + 1][r - 1] : 0;
// 4种情况PK一下
dp[l][r] = Math.max(Math.max(p1, p2), Math.max(p3, p4));
}
}
// return process(chs, 0, chs.length - 1);
return dp[0][N - 1];
}
}
/**
* 暴力递归版本
*/
/*class Solution {
public int longestPalindromeSubseq(String s) {
char[] chs = s.toCharArray();
return process(chs, 0, chs.length - 1);
}
private int process(char[] chs, int l, int r) {
// 剩一个字符
if (l == r) return 1;
// 剩两个字符
if (l == r - 1) return chs[l] == chs[r] ? 2 : 0;
// 不要l字符和r字符
int p1 = process(chs, l + 1, r - 1);
// 不要l字符
int p2 = process(chs, l + 1, r);
// 不要r字符
int p3 = process(chs, l, r - 1);
// l字符和r字符相等,要
int p4 = chs[l] == chs[r] ? 2 + process(chs, l + 1, r - 1) : 0;
// 4种情况PK一下
return Math.max(Math.max(p1, p2), Math.max(p3, p4));
}
}*/
}
11、最小距离累加和
给定一个二维数组matrix,一个人必须从左上角出发,最后达到右下角
沿途只可以向下或者向右走,沿途的数字都累加就是距离累加和
返回最小距离累加和
/**
* 给定一个二维数组matrix,一个人必须从左上角出发,最后达到右下角
* 沿途只可以向下或者向右走,沿途的数字都累加就是距离累加和
* 返回最小距离累加和
* Created by huangjunyi on 2022/11/27.
*/
public class DynamicProgramming11 {
/**
* 动态规划
* @param matrix
* @return
*/
public static int getMinPathSum01(int[][] matrix) {
if (matrix == null || matrix.length == 0 || matrix[0] == null || matrix[0].length == 0) return 0;
int N = matrix.length;
int M = matrix[0].length;
// dp[i][j] 走左上角出发,走到i行j列的格子,最小距离累加和是多少
int[][] dp = new int[N][M];
// 初始化第0行
dp[0][0] = matrix[0][0];
for (int i = 1; i < M; i++) {
dp[0][i] = dp[0][i - 1] + matrix[0][i];
}
// dp[i][j] 从左边走过来(dp[i][j-1]),从上边走过来(dp[i-1][j]),两个方向,选最路径和最短
for (int i = 1; i < N; i++) {
dp[i][0] = dp[i - 1][0] + matrix[i][0];
for (int j = 1; j < M; j++) {
dp[i][j] = Math.min(dp[i][j-1], dp[i-1][j]) + matrix[i][j];
}
}
return dp[N - 1][M - 1];
}
/**
* 动态规划,空间压缩
* @param matrix
* @return
*/
public static int getMinPathSum02(int[][] matrix) {
if (matrix == null || matrix.length == 0 || matrix[0] == null || matrix[0].length == 0) return 0;
int N = matrix.length;
int M = matrix[0].length;
// 因为dp[i][j]只依赖左边和上边一个格子,所以不需要二维dp表,一位表滚动更新即可
int[] dp = new int[M];
// 初始化第0行
dp[0] = matrix[0][0];
for (int i = 1; i < M; i++) {
dp[i] = dp[i - 1] + matrix[0][i];
}
/*
假设滚动更新到i行,现在要填dp[j],此时还没更新dp[j],那么:
dp[j-1] 对应 dp[i][j-1]
dp[j] 对应 dp[i-1][j]
dp[j] = Math.min(dp[j-1], dp[j]) + matrix[i][j];
*/
for (int i = 1; i < N; i++) {
dp[0] = dp[0] + matrix[i][0];
for (int j = 1; j < M; j++) {
dp[j] = Math.min(dp[j-1], dp[j]) + matrix[i][j];
}
}
return dp[M - 1];
}
}
12、货币组合问题2
货币组合问题2
给定一个整形数组arr,表示一组货币
数组每个值都是一张货币
但是值相同的货币没有任何不同
给定一个整形aim,表示需要通过不同的货币拼凑一起到总额aim
从arr中取货币
求有多少种组合方法
例如:arr = [1,2,1,1,2,1,2],aim = 4
方法:1+1+1+1、1+1+2、2+2
/**
* 货币组合问题2
* 给定一个整形数组arr,表示一组货币
* 数组每个值都是一张货币
* 但是值相同的货币没有任何不同
* 给定一个整形aim,表示需要通过不同的货币拼凑一起到总额aim
* 从arr中取货币
* 求有多少种组合方法
*
* 例如:arr = [1,2,1,1,2,1,2],aim = 4
* 方法:1+1+1+1 1+1+2 2+2
* Created by huangjunyi on 2022/9/3.
*/
public class DynamicProgramming12 {
/**
* 暴力递归
* @param arr 货币数组
* @param aim 目标总额
* @return 方法数
*/
public static int method01(int[] arr, int aim) {
if (arr == null || arr.length == 0 || aim < 0) return 0;
// key:货币面值,value:货币张数
Map<Integer, Integer> map = new HashMap<>();
for (int i = 0; i < arr.length; i++) {
if (map.containsKey(arr[i])) map.put(arr[i], map.get(arr[i]) + 1);
else map.put(arr[i], 1);
}
// 货币面值数组
int[] money = new int[map.size()];
// 货币张数数组
int[] count = new int[map.size()];
int index = 0;
// 根据map初始化money和count数组
for (Map.Entry<Integer, Integer> entry : map.entrySet()) {
money[index] = entry.getKey();
count[index] = entry.getValue();
index++;
}
return process01(money, count, 0, aim);
}
/**
* 暴力递归
* @param money 货币面值数组
* @param count 货币张数数组
* @param index 第index号货币开始,往后的货币,自由选择
* @param rest 剩余要凑够的钱
* @return 方法数
*/
private static int process01(int[] money, int[] count, int index, int rest) {
if (index == money.length) return rest == 0 ? 1 : 0;
int res = 0;
// index号货币,使用0张,使用1张,使用2张,......,使用count[index]张
for (int i = 0; rest - money[index] * i >= 0 && i <= count[index]; i++) {
res += process01(money, count, index + 1, rest - money[index] * i);
}
return res;
}
/**
* 动态规划
* @param arr 货币数组
* @param aim 目标总额
* @return 方法数
*/
public static int method02(int[] arr, int aim) {
if (arr == null || arr.length == 0 || aim < 0) return 0;
// key:货币面值,value:货币张数
Map<Integer, Integer> map = new HashMap<>();
for (int i = 0; i < arr.length; i++) {
if (map.containsKey(arr[i])) map.put(arr[i], map.get(arr[i]) + 1);
else map.put(arr[i], 1);
}
// 货币面值数组
int[] money = new int[map.size()];
// 货币张数数组
int[] count = new int[map.size()];
int index = 0;
// 根据map初始化money和count数组
for (Map.Entry<Integer, Integer> entry : map.entrySet()) {
money[index] = entry.getKey();
count[index] = entry.getValue();
index++;
}
/*
暴力递归2个可变参数,二维表,观察可变参数范围,确定dp表的长度
dp[index][rest] index号货币开始往后自由选择,凑够rest元,的方法数
*/
int[][] dp = new int[money.length + 1][aim + 1];
// 根据 base case 初始化dp表:if (index == money.length) return rest == 0 ? 1 : 0;
dp[money.length][0] = 1;
/*
index号货币,使用0张,使用1张,使用2张,......,使用count[index]张
for (int i = 0; rest - money[index] * i >= 0 && i <= count[index]; i++) {
res += process01(money, count, index + 1, rest - money[index] * i);
}
*/
for (index = money.length - 1; index >= 0; index--) {
for (int rest = 0; rest <= aim; rest++) {
int res = 0;
for (int i = 0; rest - money[index] * i >= 0 && i <= count[index]; i++) {
res += dp[index + 1][rest - money[index] * i];
}
dp[index][rest] = res;
}
}
// return process01(money, count, 0, aim);
return dp[0][aim];
}
/**
* 动态规划 枚举优化
* @param arr 货币数组
* @param aim 目标总额
* @return 方法数
*/
public static int method03(int[] arr, int aim) {
if (arr == null || arr.length == 0 || aim < 0) return 0;
Map<Integer, Integer> map = new HashMap<>();
for (int i = 0; i < arr.length; i++) {
if (map.containsKey(arr[i])) map.put(arr[i], map.get(arr[i]) + 1);
else map.put(arr[i], 1);
}
int[] money = new int[map.size()];
int[] count = new int[map.size()];
int index = 0;
for (Map.Entry<Integer, Integer> entry : map.entrySet()) {
money[index] = entry.getKey();
count[index] = entry.getValue();
index++;
}
int[][] dp = new int[money.length + 1][aim + 1];
dp[money.length][0] = 1;
for (index = money.length - 1; index >= 0; index--) {
for (int rest = 0; rest <= aim; rest++) {
/*
观察:
假设count[index] = 3,index号货币有3张
dp[index][rest] = dp[index + 1][rest] + dp[index + 1][rest - 1 * money[index]] + dp[index + 1][rest - 2 * money[index]] + dp[index + 1][rest - 3 * money[index]]
dp[index][rest - 1 * money[index]] = dp[index + 1][rest - 1 * money[index]] + dp[index + 1][rest - 2 * money[index]] + dp[index + 1][rest - 3 * money[index]] + dp[index + 1][rest - 4 * money[index]]
所以:
dp[index][rest] = dp[index + 1][rest] + dp[index][rest - 1 * money[index]] - dp[index + 1][rest - 4 * money[index]];
dp[index][rest] = dp[index + 1][rest] + dp[index][rest - 1 * money[index]] - dp[index + 1][rest - (count[index] + 1) * money[index]];
*/
dp[index][rest] = dp[index + 1][rest];
if (rest - money[index] >= 0) dp[index][rest] += dp[index][rest - money[index]];
if (rest - (count[index] + 1) * money[index] >= 0) dp[index][rest] -= dp[index + 1][rest - (count[index] + 1) * money[index]];
}
}
return dp[0][aim];
}
public static void main(String[] args) {
int[] arr = {
1,2,1,1,2,1,2};
int aim = 4;
System.out.println(method01(arr, aim));
System.out.println(method02(arr, aim));
System.out.println(method03(arr, aim));
}
}
13、英雄打怪兽
给定三个参数,N、M、K
怪兽有N滴血,等着英雄来砍自己
英雄每一次打击,都会让怪兽流失[0-M]的血量
到底流失多少?每一次在[0-M]上等概率的获得一个值
求K次打击之后,英雄把怪兽砍死的概率
/**
* 给定三个参数,N、M、K
* 怪兽有N滴血,等着英雄来砍自己
* 英雄每一次打击,都会让怪兽流失[0-M]的血量
* 到底流失多少?每一次在[0-M]上等概率的获得一个值
* 求K次打击之后,英雄把怪兽砍死的概率
* Created by huangjunyi on 2022/11/28.
*/
public class DynamicProgramming13 {
/**
* 暴力递归
* @param N 怪兽有N滴血
* @param M 怪兽流失血量范围
* @param K 英雄打击K次
* @return
*/
public static double killMonster01(int N, int M, int K) {
if (N < 1 || M < 1 || K < 1) return 0;
// 所有情况数
long all = (long) Math.pow(M + 1, K);
// 砍死怪兽的情况数
long kill = process01(N, M, K);
return ((double) kill) / ((double) all);
}
/**
* 暴力递归
* @param hp 怪兽剩余血量
* @param M 怪兽流失血量范围
* @param rest 英雄剩K次要砍
* @return
*/
private static long process01(int hp, int M, int rest) {
// base case:砍完了,怪兽血量减到0以下,返回1中有效方法数
if (rest == 0) return hp <= 0 ? 1 : 0;
// 怪兽已经死了,也要继续砍,因为往后的都是算入有效方法数的
if (hp <= 0) return (long) Math.pow(M + 1, rest);
// 枚举砍出的伤害值,累加方法数
long ways = 0;
for (int i = 0; i <= M; i++) {
ways += process01(hp - i, M, rest - 1);
}
return ways;
}
/**
* 动态规划
* @param N 怪兽有N滴血
* @param M 怪兽流失血量范围
* @param K 英雄打击K次
* @return
*/
public static double killMonster02(int N, int M, int K) {
if (N < 1 || M < 1 || K < 1) return 0;
// 所有情况数
long all = (long) Math.pow(M + 1, K);
/*
暴力递归两个可变参数,剩余要砍次数、怪兽剩余血量,所以是一张二维dp表
dp[rest][hp]
英雄剩余要看rest次,怪兽剩余血量hp,砍死怪兽的方法数
观察暴力递归的参数范围,可得dp表长度
*/
long[][] dp = new long[K + 1][N + 1];
/*
根据base case,初始化dp表:
if (rest == 0) return hp <= 0 ? 1 : 0;
if (hp <= 0) return (long) Math.pow(M + 1, rest);
*/
dp[0][0] = 1;
for (int rest = 1; rest <= K; rest++) {
dp[rest][0] = (long) Math.pow(M + 1, rest);
}
/*
观察暴力递归中,外层递归与里层递归的依赖关系
确定dp表的填表顺序
long ways = 0;
for (int i = 0; i < M; i++) {
ways += process01(hp - i, M, rest - 1);
}
dp[rest][...] 依赖 dp[rest - 1][...]
所以是从上往下填
*/
for (int rest = 1; rest <= K; rest++) {
for (int hp = 1; hp <= N; hp++) {
long ways = 0;
for (int i = 0; i <= M; i++) {
// 这里要注意hp减完有可能越界,越界了就通过公式算
ways += hp - i >= 0 ? dp[rest - 1][hp - i] : (long) Math.pow(M + 1, rest - 1);
}
dp[rest][hp] = ways;
}
}
/*
根据暴力递归的最外层递归,确定返回值
long kill = process01(N, M, K);
return ((double) kill) / ((double) all);
*/
return ((double) dp[K][N]) / ((double) all);
}
/**
* 动态规划 枚举行为优化
* @param N 怪兽有N滴血
* @param M 怪兽流失血量范围
* @param K 英雄打击K次
* @return
*/
public static double killMonster03(int N, int M, int K) {
if (N < 1 || M < 1 || K < 1) return 0;
long all = (long) Math.pow(M + 1, K);
long[][] dp = new long[K + 1][N + 1];
dp[0][0] = 1;
for (int rest = 1; rest <= K; rest++) {
dp[rest][0] = (long) Math.pow(M + 1, rest);
}
for (int rest = 1; rest <= K; rest++) {
for (int hp = 1; hp <= N; hp++) {
// long ways = 0;
// for (int i = 0; i < M; i++) {
// // 这里要注意hp减完有可能越界,越界了就通过公式算
// ways += hp - i >= 0 ? dp[hp - i][rest - 1] : (long) Math.pow(M + 1, rest - 1);
// }
// dp[rest][hp] = ways;
/*
有枚举行为,就随便算一个格子看依赖关系就行了
观察dp[5][10],M=5,英雄剩5次要砍,怪兽剩10点血
dp[5][10] = dp[4][5...10]
dp[5][11] = dp[4][6...11]
所以:
dp[5][11] = dp[4][11] + dp[5][10] - dp[4][5]
推断出:
dp[rest][hp] = dp[rest - 1][hp] + dp[rest][hp - 1] - dp[rest - 1][hp - M - 1]
但是那是hp - M - 1不越界的情况,如果越界:
dp[rest][hp] = dp[rest - 1][hp] + dp[rest][hp - 1] - (long) Math.pow(M + 1, rest - 1)
*/
dp[rest][hp] = dp[rest][hp - 1] + dp[rest - 1][hp];
if (hp - 1 - M >= 0) {
dp[rest][hp] -= dp[rest - 1][hp - 1 - M];
} else {
dp[rest][hp] -= Math.pow(M + 1, rest - 1);
}
}
}
return ((double) dp[K][N]) / ((double) all);
}
public static void main(String[] args) {
System.out.println("begin");
for (int i = 0; i < 20000; i++) {
int N = (int) (Math.random() * 10);
int M = (int) (Math.random() * 10);
int K = (int) (Math.random() * 10);
double res1 = killMonster01(N, M, K);
double res2 = killMonster02(N, M, K);
double res3 = killMonster03(N, M, K);
if (res1 != res2 || res1 != res3) {
System.out.println("error: " + " N=" + N + " M=" + M + " K=" + K);
System.out.println("res1=" + res1 + " res2=" + res2 + " res3=" + res3);
break;
}
}
System.out.println("finished");
}
}
14、货币组合问题3
arr是面值数组,其中的值都是正数且没有重复。
再给定一个正数aim。
每个值都认为是一种面值,且认为张数是无限的。
返回组成aim的最少货币数。
/**
* 货币组合问题3
* arr是面值数组,其中的值都是正数且没有重复。
* 再给定一个正数aim。
* 每个值都认为是一种面值,且认为张数是无限的。
* 返回组成aim的最少货币数。
*
* Created by huangjunyi on 2022/11/30.
*/
public class DynamicProgramming14 {
/**
* 暴力递归
*/
public static int minCoins01(int[] arr, int aim) {
return process(arr, 0, aim);
}
/**
* 暴力递归
* @param arr 货币数组
* @param index 当前货币
* @param rest 剩余要凑够的钱数
* @return
*/
private static int process(int[] arr, int index, int rest) {
// base case 货币都决定完了,剩余要凑够的钱数为0,返回0(代表凑够0元需要0张货币),否则返回MAX,代表无效
if (index == arr.length) return rest == 0 ? 0 : Integer.MAX_VALUE;
int min = Integer.MAX_VALUE;
// index号货币要0张,要1张,要2张......拿最少值
for (int i = 0; i * arr[index] <= rest; i++) {
int next = process(arr, index + 1, rest - i * arr[index]);
if (next != Integer.MAX_VALUE) min = Math.min(min, next + i);
}
return min;
}
/**
* 动态规划
* @param arr 货币数组
* @param aim 要凑够的目标货币数
* @return
*/
public static int minCoins02(int[] arr, int aim) {
/*
根据暴力递归,可变参数的个数,范围,推测dp表的结构
可变参数:index rest => 二维dp表
范围:index:0~arr.length rest: 0~aim
dp[index][rest] 从index号货币开始往后自由选择,凑出rest元的最少货币数
*/
int[][] dp = new int[arr.length + 1][aim + 1];
// 根据暴力递归 base case 初始化dp表
// if (index == arr.length) return rest == 0 ? 1 : Integer.MAX_VALUE;
dp[arr.length][0] = 0;
for (int i = 1; i <= aim; i++) {
dp[arr.length][i] = Integer.MAX_VALUE;
}
/*
观察暴力递归外层与内层的依赖关系,确定填表的方向
int min = Integer.MAX_VALUE;
// index号货币要0张,要1张,要2张......拿最少值
for (int i = 0; i * arr[index] <= rest; i++) {
int next = process(arr, index + 1, rest - i * arr[index]);
if (next != Integer.MAX_VALUE) min = Math.min(min, next + i);
}
index 依赖 index + 1
所以从下往上填
*/
for (int index = arr.length - 1; index >= 0; index--) {
for (int rest = 1; rest <= aim; rest++) {
int min = Integer.MAX_VALUE;
// index号货币要0张,要1张,要2张......拿最少值
for (int i = 0; i * arr[index] <= rest; i++) {
int next = dp[index + 1][rest - i * arr[index]];
if (next != Integer.MAX_VALUE) min = Math.min(min, next + i);
}
dp[index][rest] = min;
}
}
// 根据暴力递归最外层递归的参数,确定返回值
// return process(arr, 0, aim);
return dp[0][aim];
}
/**
* 动态规划 枚举行为优化
* @param arr 货币数组
* @param aim 要凑够的目标货币数
* @return
*/
public static int minCoins03(int[] arr, int aim) {
int[][] dp = new int[arr.length + 1][aim + 1];
dp[arr.length][0] = 0;
for (int i = 1; i <= aim; i++) {
dp[arr.length][i] = Integer.MAX_VALUE;
}
for (int index = arr.length - 1; index >= 0; index--) {
for (int rest = 1; rest <= aim; rest++) {
/*int min = Integer.MAX_VALUE;
for (int i = 0; i * arr[index] <= rest; i++) {
int next = dp[index + 1][rest - i * arr[index]];
if (next != Integer.MAX_VALUE) min = Math.min(min, next + i);
}
dp[index][rest] = min;*/
/*
观察dp[5][10] 假设arr[5]=3:
dp[5][10] = Math.min(dp[6][10], dp[6][7] + 1, dp[6][4] + 2, dp[6][1] + 3)
dp[5][7] = Math.min( dp[6][7], dp[6][4] + 1, dp[6][1] + 2)
所以:
dp[5][10] = Math.min(dp[6][10], dp[5][7] + 1)
dp[index][rest] = Math.min(dp[index + 1][rest], dp[index][rest- arr[index]] + 1)
*/
dp[index][rest] = dp[index + 1][rest];
if (rest- arr[index] >= 0 && dp[index][rest- arr[index]] != Integer.MAX_VALUE) {
dp[index][rest] = Math.min(dp[index][rest], dp[index][rest- arr[index]] + 1);
}
}
}
return dp[0][aim];
}
}
15、数字切分
给你一个数字num,将它切开
比如给你7,你可以切成2/2/3,也可以切成3/4,但是不能切成3/2/2或4/3,也就是前面的数不能大于后面的数
返回一个数一共有多少中切分方法
/**
* 数字切分
* 给你一个数字num,将它切开
* 比如给你7,你可以切成2/2/3,也可以切成3/4,但是不能切成3/2/2或4/3,也就是前面的数不能大于后面的数
* 返回一个数一共有多少中切分方法
* Created by huangjunyi on 2022/11/30.
*/
public class DynamicProgramming15 {
/**
* 暴力递归
* @param n 要切分的数字
*/
public static int splitNumber01(int n) {
if (n == 0) return 0;
if (n == 1) return 1;
return process(1, n);
}
/**
* 暴力递归
* 前一个数字是preNum,剩下要切分的数字是restNum,切分restNum的切分方法数
* @param preNum 前一个数字
* @param restNum 剩下要切分的数字
* @return
*/
private static int process(int preNum, int restNum) {
// restNum切成了0,有效切分方法数1
if (restNum == 0)return 1;
// 前一个数比restNum,无效切分
if (preNum > restNum) return 0;
// 当前切出preNum,切出preNum+1,切出preNum+2......,方法数累加
int ways = 0;
for (int i = preNum; i <= restNum; i++) {
ways += process(i, restNum - i);
}
return ways;
}
/**
* 动态规划
* @param n 要切分的数字
* @return
*/
private static int splitNumber02(int n) {
/*
观察暴力递归的可变参数个数,已经可变参数范围
preNum:1~n
restNum:0~n
dp[preNum][restNum]
前一个数字是preNum,剩下要切分的数字是restNum,切分restNum的切分方法数
*/
int[][] dp = new int[n + 1][n + 1];
/*
根据暴力递归的base case初始化dp表
if (restNum == 0)return 1;
if (preNum > restNum) return 0;
*/
for (int preNum = 1; preNum <= n; preNum++) {
dp[preNum][0] = 1;
}
/*
观察暴力递归的外层递归和内层递归的依赖关系,确定dp表的填写顺序
int ways = 0;
for (int i = preNum; i <= restNum; i++) {
ways += process(i, restNum - i);
}
return ways;
preNum依赖preNum+1、preNum+2......
所以从下往上填
因为preNum > restNum 都是无效的,所以只需要填上半部分
*/
for (int preNum = n; preNum >= 1; preNum--) {
for (int restNum = preNum; restNum <= n; restNum++) {
int ways = 0;
for (int i = preNum; i <= restNum; i++) {
ways += dp[i][restNum - i];
}
dp[preNum][restNum] = ways;
}
}
// 根据暴力递归的最外层递归确定返回值
// return process(1, n);
return dp[1][n];
}
/**
* 动态规划 枚举行为优化
* @param n 要切分的数字
* @return
*/
private static int splitNumber03(int n) {
int[][] dp = new int[n + 1][n + 1];
for (int preNum = 1; preNum <= n; preNum++) {
dp[preNum][0] = 1;
}
for (int preNum = n; preNum >= 1; preNum--) {
for (int restNum = preNum; restNum <= n; restNum++) {
/*int ways = 0;
for (int i = preNum; i <= restNum; i++) {
ways += dp[i][restNum - i];
}
dp[preNum][restNum] = ways;*/
/*
观察dp[2][10]
dp[2][10] = dp[2][8] + dp[3][7] + dp[4][6] + dp[5][5]
dp[3][10] = dp[3][7] + dp[4][6] + dp[5][5]
所以:
dp[2][10] = dp[2][8] + dp[3][10]
dp[preNum][restNum] = dp[preNum][restNum - preNum] + dp[preNum + 1][restNum]
*/
dp[preNum][restNum] = dp[preNum][restNum - preNum];
if (preNum != n) dp[preNum][restNum] += dp[preNum + 1][restNum];
}
}
return dp[1][n];
}
public static void main(String[] args) {
int n = 68;
System.out.println(splitNumber01(n));
System.out.println(splitNumber02(n));
System.out.println(splitNumber03(n));
}
}
16、较小集合的累加和
给定一个正数数组arr
请把arr中所有的数分成两个集合,尽量让两个集合的累加和接近
返回: 最接近的情况下,较小集合的累加和
/**
* 较小集合的累加和
* 给定一个正数数组arr
* 请把arr中所有的数分成两个集合,尽量让两个集合的累加和接近
* 返回:
* 最接近的情况下,较小集合的累加和
* Created by huangjunyi on 2022/11/30.
*/
public class DynamicProgramming16 {
/**
* 暴力递归
*/
public static int smallSum01(int[] arr) {
if (arr == null || arr.length <= 1) return 0;
int sum = 0;
for (int num : arr) {
sum += num;
}
// arr数组累加和除以2,把题意转换为从arr数组自由选择,
// 返回最接近但是不超过arr累加和一半的集合累加和
return process(arr, 0 , sum / 2);
}
/**
* 暴力递归,把题意转换为从index位置,arr后面的数只有做选择,返回最近但是不超过rest的数
*/
private static int process(int[] arr, int index, int rest) {
// base case 没有数需要选择了,返回0
if (index == arr.length) return 0;
// 不要index位置的数
int p1 = process(arr, index + 1, rest);
// 要index位置的数,但是要判断不能超过rest
int p2 = 0;
if (arr[index] <= rest) {
p2 = arr[index] + process(arr, index + 1, rest - arr[index]);
}
return Math.max(p1, p2);
}
public static int smallSum02(int[] arr) {
if (arr == null || arr.length <= 1) return 0;
/*
可变参数index,rest
index:0 ~ arr.length
rest: 0 ~ sum/2
*/
int sum = 0;
for (int num : arr) sum += num;
int[][] dp = new int[arr.length + 1][(sum / 2) + 1];
// base case: if (index == arr.length) return 0;
// 数组初始值本身就是0,不用初始化
/*
暴力递归中外层与内层的依赖关系
// 不要index位置的数
int p1 = process(arr, index + 1, rest);
// 要index位置的数,但是要判断不能超过rest
int p2 = 0;
if (arr[index] <= rest) {
p2 = arr[index] + process(arr, index + 1, rest - arr[index]);
}
return Math.max(p1, p2);
所以index依赖index+1
所以从下往上填
*/
for (int index = arr.length - 1; index >= 0; index--) {
for (int rest = 0; rest <= sum / 2; rest++) {
// 不要index位置的数
int p1 = dp[index + 1][rest];
// 要index位置的数,但是要判断不能超过rest
int p2 = 0;
if (arr[index] <= rest) {
p2 = arr[index] + dp[index + 1][rest - arr[index]];
}
dp[index][rest] = Math.max(p1, p2);
}
}
// 暴力递归最外层:return process(arr, 0 , sum / 2);
return dp[0][sum / 2];
}
}
17、较小集合的累加和2
给定一个正整数数组arr,请把arr中所有的数分成两个集合
如果arr长度为偶数,两个集合包含数的个数要一样多
如果arr长度为奇数,两个集合包含数的个数必须只差一个
请尽量让两个集合的累加和接近
返回: 最接近的情况下,较小结合的累加和
/**
* 给定一个正整数数组arr,请把arr中所有的数分成两个集合
* 如果arr长度为偶数,两个集合包含数的个数要一样多
* 如果arr长度为奇数,两个集合包含数的个数必须只差一个
* 请尽量让两个集合的累加和接近
* 返回:
* 最接近的情况下,较小结合的累加和
* Created by huangjunyi on 2022/11/30.
*/
public class DynamicProgramming17 {
/**
* 暴力递归
*/
public static int smallSum01(int[] arr) {
if (arr == null || arr.length <= 1) return 0;
int sum = 0;
for (int num : arr) {
sum += num;
}
if ((arr.length & 1) == 0) {
return process(arr, 0, arr.length / 2, sum / 2);
} else {
return Math.max(process(arr, 0, arr.length / 2, sum / 2), process(arr, 0, arr.length / 2 + 1, sum / 2));
}
}
/**
* 从index位置开始,在数组arr中只有挑选数字,必须挑满picks个,
* 返回最接近rest但是不超过rest的集合累加和
*/
private static int process(int[] arr, int index, int picks, int rest) {
// base case:没数了,看挑完没,没挑完要返回-1,表示无效
if (index == arr.length) return picks == 0 ? 0 : -1;
// index的数不要
int p1 = process(arr, index + 1, picks, rest);
// index的数要
int p2 = -1;
int next = -1;
if (arr[index] <= rest) next = process(arr, index + 1, picks - 1, rest - arr[index]);
if (next != -1) p2 = arr[index] + next;
// 两个累加和PK一下
return Math.max(p1, p2);
}
/**
* 动态规划
*/
public static int smallSum02(int[] arr) {
if (arr == null || arr.length <= 1) return 0;
int sum = 0;
for (int num : arr) {
sum += num;
}
/*
可变参数:index picks rest
index:0 ~ arr.length
picks: 偶数 0 ~ arr.length / 2 奇数 0 ~ arr.length / 2 + 1
rest: 0 ~ sum / 2
dp[index][picks][rest]:从index位置开始,在数组arr中只有挑选数字,必须挑满picks个,最接近rest但是不超过rest的集合累加和
*/
int[][][] dp = new int[arr.length + 1][(arr.length + 1) / 2 + 1][sum / 2 + 1];
/*
根据base case 初始化dp表
// base case:没数了,看挑完没,没挑完要返回-1,表示无效
if (index == arr.length) return picks == 0 ? 0 : -1;
*/
for (int index = 0; index <= arr.length; index++) {
for (int picks = 0; picks <= (arr.length + 1) / 2; picks++) {
for (int rest = 0; rest <= sum / 2; rest++) {
dp[index][picks][rest] = -1;
}
}
}
for (int rest = 0; rest <= sum / 2; rest++) {
dp[arr.length][0][rest] = 0;
}
/*
暴力递归外层与内层的依赖关系:
// index的数不要
int p1 = process(arr, index + 1, picks, rest);
// index的数要
int p2 = -1;
int next = -1;
if (arr[index] <= rest) next = process(arr, index + 1, picks - 1, rest - arr[index]);
if (next != -1) p2 = arr[index] + next;
// 两个累加和PK一下
return Math.max(p1, p2);
index层依赖于index+1层,所以从下往上填
*/
for (int index = arr.length - 1; index >= 0; index--) {
for (int picks = 0; picks <= (arr.length + 1) / 2; picks++) {
for (int rest = 0; rest <= sum / 2; rest++) {
// index的数不要
int p1 = dp[index + 1][picks][rest];
// index的数要
int p2 = -1;
int next = -1;
if (arr[index] <= rest && picks > 0) next = dp[index + 1][picks - 1][rest - arr[index]];
if (next != -1) p2 = arr[index] + next;
// 两个累加和PK一下
dp[index][picks][rest] = Math.max(p1, p2);
}
}
}
// 根据暴力递归的最外层,确定返回值
if ((arr.length & 1) == 0) {
return dp[0][arr.length / 2][sum / 2];
} else {
return Math.max(dp[0][arr.length / 2][sum / 2], dp[0][arr.length / 2 + 1][sum / 2]);
}
}
}
总结
什么题目能用动态规划写
只要一个题目可以使用递归解,而且在递归的过程中,出现了求重复解的情况,就可以优化为动态规划,前提是递归过程的可变参数不会过于复杂(比如数组类型,集合类型)
递归如何优化为动态规划
1、 根据递归的可变参数确定动态规划dp表的维度,一个可变参数,就是一维表,两个可变参数,就是二维表;
2、 根据递归的可变参数的范围,确定dp表的大小;
3、 dp表一个格子代表的含义,就是一层递归的返回值代表的含义;
4、 dp表定好后,根据递归的终止条件(basecase),初始化dp表;
5、 根据外层递归与内层递归的依赖关系,确定dp表的填写顺序;
6、 如果存在枚举行为观察临近格子与当前格子,是否存在重复枚举的部分,如果有,则可以进行枚举行为优化;
7、 根据最外层递归的可变参数的值,确定以dp表中哪个格子作为返回值;
枚举行为优化
存在枚举行为是指递归里面存在for循环嵌套递归来计算本层递归的返回值,或者填dp表某个格子时存在for循环遍历其他格子计算当前格子的值的行为。
如何进行枚举行为的优化?
1、 观察某个格子,计算这个格子的值需要依赖到其他哪些格子;
2、 再观察这个格子的临近的格子(上下左右),计算这个格子的值需要依赖到其他哪些格子;
3、 对比这两个格子,在计算的时候,所依赖的其他格子,是否用重复的部分;
4、 如果有,则可以通过复用临近的这个格子的值(可能要减掉多余的部分),替代掉枚举行为;
空间压缩
比如在填二维dp表的时候,发现填本行时,只依赖到上一行,可以尝试把二维dp表优化为一维表(但不一定可以,要看依赖到哪些格子)
递归的几种尝试模型
1、 从左往右的尝试模型;
比如题目17“较小集合的累加和”,从左往右依次遍历,每一个位置保留和不保留,得出不同结果,这种尝试模型,就是从左往右
2、 一个样本做行,一个样本做列;
比如题目7“求两个字符串的最长公共子序列长度”,两个字符串都是一个样本,要枚举两个字符串不同长度时的情况,得出不同结果,这种尝试模型,就是“一个样本做行,一个样本做列”
3、 范围尝试模型;
比如题目10“最长回文子序列”,在某个范围上进行尝试,通常这种在填dp表时左下半区的dp表是不用填的
4、 业务限制的尝试模型;
什么是参数过于复杂,不能用动态规划?比如N皇后问题
N皇后问题是指在N*N的棋盘上要摆N个皇后,
要求任何两个皇后不同行、不同列,也不在同一条斜线上
给定一个正数n,返回n皇后的摆法有多少种。
n=1,返回1
n=2或3,2皇后和3皇后问题无论怎么摆都不行,返回0
n=8,返回92
/**
* N皇后问题
*
* N皇后问题是指在N*N的棋盘上要摆N个皇后,
* 要求任何两个皇后不同行、不同列,也不在同一条斜线上
* 给定一个正数n,返回n皇后的摆法有多少种。
* n=1,返回1
* n=2或3,2皇后和3皇后问题无论怎么摆都不行,返回0
* n=8,返回92
*
* 需要用递归,但是不能优化为动态规划的例子
*
* Created by huangjunyi on 2022/11/30.
*/
public class DynamicProgramming18 {
public static int ways(int n) {
if (n < 1) return 0;
// record[i]表示在第i行的皇后摆在第几列
int[] record = new int[n];
return process(n, record, 0);
}
private static int process(int n, int[] record, int i) {
// 来到第n行,表示全都摆好了,返回一种可行方法数
if (i == n) return 1;
int res = 0;
// 放在第1列,放在第2列...,累加方法数
for (int j = 0; j < n; j++) {
// 摆在该列是否违规,违规则跳过,当前行只与往上的行进行比较,不用管下面的行,下面的行交给下层递归
boolean flag = true;
for (int k = 0; k < i; k++) {
if (j == record[k] || Math.abs(record[k] - j) == Math.abs(i - k)) {
flag = false;
break;
}
}
// 记录:第i行的皇后,摆在j列
if (flag) {
record[i] = j;
res += process(n, record, i + 1);
}
}
return res;
}
}
因为可变参数中存在一个record 数组,是无法改为dp表的,或者强行改成dp表会非常的复杂,因为这个record数组有很多种情况,无法像整形那样很简单的确定范围