07、算法与数据结构 - 实战:前缀树,计数排序与桶排序
前缀树
Trie
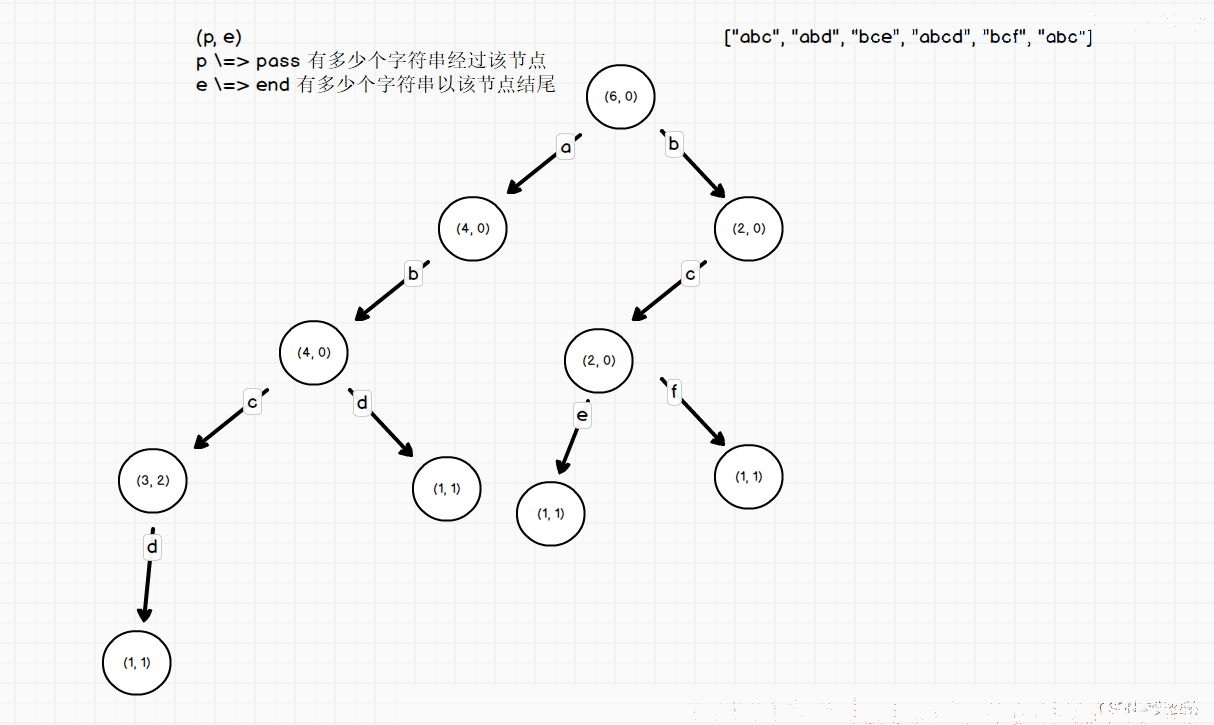
1、 根据字符串数组中,每个字符串的字符作为路径,组成而成的一个多叉树结构;
2、 每个节点都有一个paths数组,表示字符路径;
3、 每个节点都会记录有多少个字符串经过该节点,记为pass;
4、 每个节点都会记录有多少个字符串以该节点结尾,记为end;
这种结构的好处就是查询一个字符串是否存在,或者判断有多少个字符串以某个字符串作为前缀,时间复杂度是O(K),K是指该字符串的长度
/**
* 前缀树
* Created by huangjunyi on 2022/11/20.
*/
public class Trie01 {
private static class Node {
int pass; // 有多少个字符串经过该节点
int end; // 有多少个字符串以该节点结尾
Node[] paths; // 字符路径
public Node() {
pass = 0;
end = 0;
paths = new Node[26];
}
}
private Node root;
public Trie01() {
root = new Node();
}
/**
* 往前缀树中插入字符串
* @param str
*/
public void insert(String str) {
if (str == null) return;
char[] chs = str.toCharArray();
Node node = this.root;
node.pass++;
for (int i = 0; i < chs.length; i++) {
// 如果没有路,先建出路来
if (node.paths[chs[i] - 'a'] == null) node.paths[chs[i] - 'a'] = new Node();
// 沿途pass++
node.paths[chs[i] - 'a'].pass++;
node = node.paths[chs[i] - 'a'];
}
// 结尾字符路径连接的节点,end++
node.end++;
}
public void delete(String str) {
if (search(str) == 0) return;
char[] chs = str.toCharArray();
Node node = this.root;
node.pass--;
for (int i = 0; i < chs.length; i++) {
// 如果沿途发现有节点pass减到0,直接置为null,返回
if (--node.paths[chs[i] - 'a'].pass == 0) {
node.paths[chs[i] - 'a'] = null;
return;
}
node = node.paths[chs[i] - 'a'];
}
// 结尾字符路径连接的节点,end--
node.end--;
}
/**
* 一个字符串在前缀树中出现了几次
* @param str
* @return
*/
public int search(String str) {
if (str == null) return 0;
char[] chs = str.toCharArray();
Node node = this.root;
for (int i = 0; i < chs.length; i++) {
// 根据字符路径,顺着往下走,没路了就返回
if (node.paths[chs[i] - 'a'] == null) return 0;
else node = node.paths[chs[i] - 'a'];
}
// 到达终点,返回end
return node.end;
}
/**
* 一个前缀串在前缀树中出现了几次
* @param prefix
* @return
*/
public int prefixNumber(String prefix) {
if (prefix == null) return 0;
char[] chs = prefix.toCharArray();
Node node = this.root;
for (int i = 0; i < chs.length; i++) {
// 根据字符路径,顺着往下走,没路了就返回
if (node.paths[chs[i] - 'a'] == null) return 0;
else node = node.paths[chs[i] - 'a'];
}
return node.pass;
}
}
计数排序
计数排序时不基于比较的排序算法中的一种,在给定的样本范围比较小的时候,可以采用这种算法,效率会比较高
比如给定一个员工年龄数组,要求根据年龄从大到小进行排序,假设员工年龄的范围是0~200
那么定义一个长度为201的数组help,代表年龄范围,[0]表示0岁的员工有多少个,[1]表示1岁的员工有多少个
然后遍历员工数组,根据员工年龄,help数组对应的年龄+1
然后在根据help数组,把年龄拷贝回年龄数组中,就得到有序的年龄数组
时间复杂度为O(N),因为只需要遍历一遍数组

/**
* 计数排序
*/
public class CountSort01 {
public static void sort(int[] arr) {
if (arr == null || arr.length < 2) return;
//找出数组中最大的数
int max = arr[0];
for (int i = 0; i < arr.length; i++) {
max = Math.max(arr[i], max);
}
//创建一个辅助数组
int[] help = new int[max + 1];
//遍历待排序的数组,值作为help数组的下标,help数组中的值+1
for (int i = 0; i < arr.length; i++) {
help[arr[i]]++;
}
//根据help数组,把数拷贝回原数组
int index = 0;
for (int i = 0; i < help.length; i++) {
for (int j = 0; j < help[i]; j++) {
arr[index++] = i;
}
}
}
}
桶排序
普通桶排序
桶排序是计数排序的一种应用。从低数位开始直到高数位,每次遍历数组中的每一个数,以对应数位上的数作为下标,把当前数放入到该下标指定的队列中,然后在遍历每一个队列,弹出放回到原数组。
1、 按个位排序:;

2、 按十位排序;
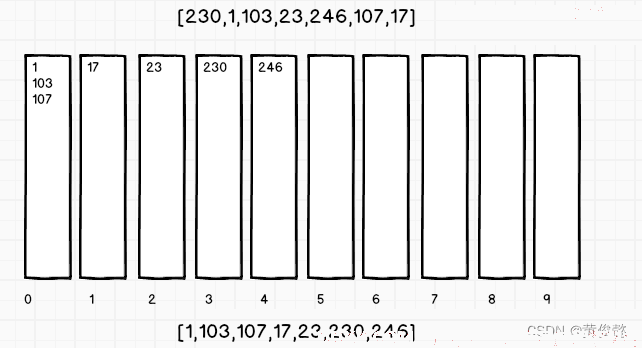
3、 按百位排序;
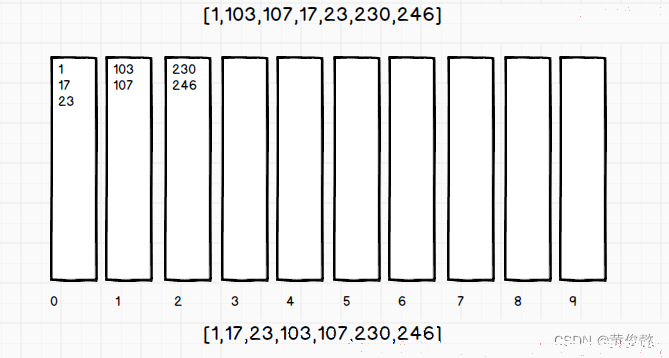
但是这种方法的比较耗费空间,需要准备十个队列,可以做出如下优化。
优化后的桶排序
1、 假设当前数位为d;
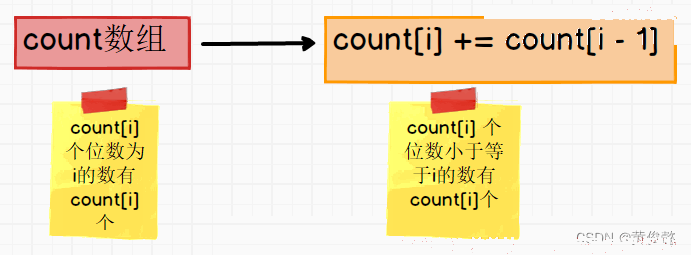
2、 遍历数组每一个数的d数位上的数,创建一个count数组,记录d数位上的数出现的次数,count[i]此时就是d数位上的数为i的出现了几次;
3、 遍历count数组,累加前缀和,count[i]此时就是d数位上的数小于等于i的,出现了几次;
4、 创建一个help数组,从后往前遍历原数组,得出d数位上的数i,然后根据count[i]得知,d数位上的数小于等于i的有count[i]个,则在数组help下标为count[i]-1的位置放入当前遍历的数,然后count[i]减一,表示d数位上的数小于等于i的还剩count[i]-1个没处理;
桶排序优化举例
现在要对数组[103,230,107,246,23,17,1]进行排序
现在先进行个位的排序
1、计算count数组
count:[1, 1, 0, 2, 0, 0, 1, 2, 0, 9]
count[0] = 1,表示个位数为0的数,有1个
count[1] = 1,表示个位数为1的数,有1个
count[2] = 0,表示个位数为2的数,有0个
… count[7] = 2,表示个位数为7的数,有2个
2、把count数组转换为前缀和数组
count:[1, 2, 2, 4, 4, 4, 5, 7, 7, 9]
count[0] = 1,表示个位数<=0的数,有1个
count[1] = 2,表示个位数<=1的数,有2个
count[2] = 2,表示个位数<=2的数,有2个
… count[7] = 7,表示个位数<=7的数,有7个
3、定义一个help数组,从后往前遍历原数组,根据count数组,确定放入help数组中的位置
遍历到1,个位数为1,count[1]=2,那么放入的位置就是1(count[1]-1 = 2-1),help[1]=1,然后count[1]–
遍历到17,个位数为7,count[7] = 7,那么放入的位置就是6(count[7]-1 = 7-1),help[6]=17,然后count[7]–
依次类推
4、然后把help数组拷贝回原数组arr
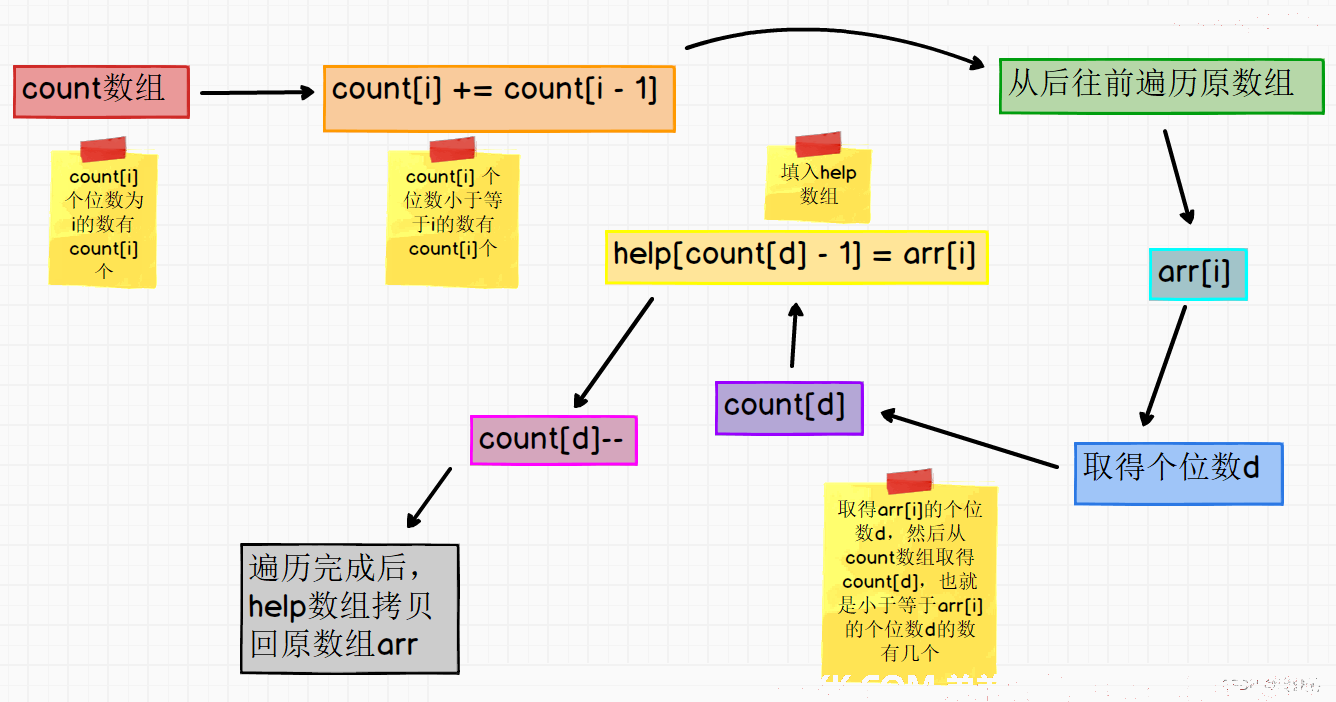
这种方式的就比真正建十个队列的方式要节省空间,只要建一个长度为10的count数组,建一个长度和原数组arr相同的help数组
代码:优化后的桶排序
/**
* 桶排序:计数排序的一种应用
*/
public class CountSort02 {
public static void sort(int[] arr) {
if (arr == null || arr.length < 2) return;
//取得当前数组最大值的位数
int maxBit = getMaxBit(arr);
//创建一个辅助数组
int[] help = new int[arr.length];
for (int i = 1; i <= maxBit; i++) {
int[] count = new int[10];
for (int j = 0; j < arr.length; j++) {
//获取数组中每个值指定位上的数
int bitNum = getBitNum(arr[j], i);
//count数组此时记录指定数位上不同数字出现的次数
count[bitNum]++;
}
for (int j = 1; j < count.length; j++) {
//count数组变成指定数位上数字小于等于j的数的个数有几个
count[j] += count[j - 1];
}
//根据count数组的记录,从原数组的最后一位往前遍历,放入help数组中的指定位置
for (int j = arr.length - 1; j >= 0; j--) {
int bitNum = getBitNum(arr[j], i);
//count[bitNum]记录了当前数位i上数字小于等于bitNum的数,出现的次数
//所以arr[j]放入到help数组中count[bitNum]-1的位置
help[count[bitNum] - 1] = arr[j];
//处理过了,减一,下次遇到指定数位上数字相同的数,就会放到前一个位置
count[bitNum]--;
}
//help数组拷贝回原数组
for (int j = 0; j < help.length; j++) {
arr[j] = help[j];
}
}
}
private static int getBitNum(int num, int bit) {
for (int i = 0; i < bit - 1; i++) {
num /= 10;
}
int help = (num / 10) * 10;
return num - help;
}
private static int getMaxBit(int[] arr) {
//找出数组中最大的数
int max = arr[0];
for (int i = 0; i < arr.length; i++) {
max = Math.max(arr[i], max);
}
int res = 0;
while (max != 0) {
max /= 10;
res++;
}
return res;
}
}